Exercise 6.6.1 z Lay: Linear Algebra and Its Applications (4th Edition).
Úloha. Nájdite priamku $y=\beta_0+\beta_1x$, ktorá najlepšie aproximuje dáta $(0,1)$, $(1,1)$, $(2,2)$, $(3,2)$.
Hľadáme $\vec\beta=(\beta_0,\beta_1)$ tak, aby $f(x)=\beta_0+\beta_1x$ bolo čo najbližšie k zadaným hodnotám. T.j. chceme minimalizovať
$$\sum_{i=1}^n (y_i-(\beta_0+\beta_1x_i))^2.$$
Vlastne vektor $(\beta_0+\beta_1x_1,\dots,\beta_0+\beta_1x_4)$ je kolmý priemet bodu $(y_1,\dots,y_4)$ na podpriestor pozostávajúci z bodov $(\beta_0+\beta_1x_1,\dots,\beta_0+\beta_1x_4)=(1,1,1,1)\beta_0+(x_1,\dots,x_4)\beta_1$, kde $\beta_0,\beta_1\in\mathbb R$.
Aproximácia lineárnou funkciou (metóda najmenších štvorcov)
Moderators: Martin Sleziak, Ludovit_Balko, Martin Niepel, Tibor Macko
-
Martin Sleziak
- Posts: 5832
- Joined: Mon Jan 02, 2012 5:25 pm
-
Martin Sleziak
- Posts: 5832
- Joined: Mon Jan 02, 2012 5:25 pm
Re: Aproximácia lineárnou funkciou (metóda najmenších štvorcov)
Nájdenie kolmého priemetu
Mám teda bod $Y=(1,1,2,2)$ a rovinu $S=[(1,1,1,1),(0,1,2,3)]$.
Chceme nájsť priemet - to vieme rátať veľa spôsobmi.
Napríklad môžeme skúsiť nájsť ortogonálnu a ortonormálnu bázu pre $S$.
Ortonogonálna báza je napríklad $\vec v_1=(1,1,1,1)$, $\vec v_2=(3,1,-1,-3)$.
Po vynormovaní máme ortonormálnu bázu $\vec u_1=\frac12(1,1,1,1)$, $\vec u_2=\frac1{2\sqrt{5}}(3,1,-1,-3)$.
Dostaneme potom maticu ortogonálnej projekcie na $S$:
$$P=
\frac1{10}
\begin{pmatrix}
7 & 4 & 1 &-2 \\
4 & 3 & 2 & 1 \\
1 & 2 & 3 & 4 \\
-2 & 1 & 4 & 7 \\
\end{pmatrix}$$
Vieme potom vypočítať kolmý priemet
$$\frac1{10}
(1,1,2,2)
\begin{pmatrix}
7 & 4 & 1 &-2 \\
4 & 3 & 2 & 1 \\
1 & 2 & 3 & 4 \\
-2 & 1 & 4 & 7 \\
\end{pmatrix}=
\frac1{10}(9,13,17,21)=(\frac{9}{10},\frac{13}{10},\frac{17}{10},\frac{21}{10})$$
Môžeme skontrolovať, že
$$(1,1,1,1)=
\underset{\in S}{\underbrace{\frac1{10}(9,13,17,21)}}+
\underset{\in S^\bot}{\underbrace{\frac1{10}(1,-3,3,-1)}}
$$
Z rovnosti $(\frac{9}{10},\frac{13}{10},\frac{17}{10},\frac{21}{10})=\frac9{10}(1,1,1,1)+\frac4{10}(0,1,2,3)$ súčasne vidím že hľadané riešenie je $\underline{\underline{(\beta_0,\beta_1)=(\frac9{10},\frac4{10})}}$.
Mám teda bod $Y=(1,1,2,2)$ a rovinu $S=[(1,1,1,1),(0,1,2,3)]$.
Chceme nájsť priemet - to vieme rátať veľa spôsobmi.
Napríklad môžeme skúsiť nájsť ortogonálnu a ortonormálnu bázu pre $S$.
Ortonogonálna báza je napríklad $\vec v_1=(1,1,1,1)$, $\vec v_2=(3,1,-1,-3)$.
Po vynormovaní máme ortonormálnu bázu $\vec u_1=\frac12(1,1,1,1)$, $\vec u_2=\frac1{2\sqrt{5}}(3,1,-1,-3)$.
Dostaneme potom maticu ortogonálnej projekcie na $S$:
$$P=
\frac1{10}
\begin{pmatrix}
7 & 4 & 1 &-2 \\
4 & 3 & 2 & 1 \\
1 & 2 & 3 & 4 \\
-2 & 1 & 4 & 7 \\
\end{pmatrix}$$
Spoiler:
$$\frac1{10}
(1,1,2,2)
\begin{pmatrix}
7 & 4 & 1 &-2 \\
4 & 3 & 2 & 1 \\
1 & 2 & 3 & 4 \\
-2 & 1 & 4 & 7 \\
\end{pmatrix}=
\frac1{10}(9,13,17,21)=(\frac{9}{10},\frac{13}{10},\frac{17}{10},\frac{21}{10})$$
Môžeme skontrolovať, že
$$(1,1,1,1)=
\underset{\in S}{\underbrace{\frac1{10}(9,13,17,21)}}+
\underset{\in S^\bot}{\underbrace{\frac1{10}(1,-3,3,-1)}}
$$
Z rovnosti $(\frac{9}{10},\frac{13}{10},\frac{17}{10},\frac{21}{10})=\frac9{10}(1,1,1,1)+\frac4{10}(0,1,2,3)$ súčasne vidím že hľadané riešenie je $\underline{\underline{(\beta_0,\beta_1)=(\frac9{10},\frac4{10})}}$.
-
Martin Sleziak
- Posts: 5832
- Joined: Mon Jan 02, 2012 5:25 pm
Re: Aproximácia lineárnou funkciou (metóda najmenších štvorcov)
Násobenie transponovanou maticou
Môžeme sa na to pozerať ako na približné riešenie sústavy:
\begin{align*}
\begin{pmatrix}
1 & x_1 \\
1 & x_2 \\
1 & x_3 \\
1 & x_4 \\
\end{pmatrix}
\begin{pmatrix}\beta_0\\\beta_1\end{pmatrix}=
\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}\\
\begin{pmatrix}
1 & 0 \\
1 & 1 \\
1 & 2 \\
1 & 3 \\
\end{pmatrix}
\begin{pmatrix}\beta_0\\\beta_1\end{pmatrix}=
\begin{pmatrix}1\\1\\2\\2\end{pmatrix}
\end{align*}
Opäť môžeme postupovať cez riešenie sústavy $A^TAB=A^TY$.
\begin{align*}
A^TA=&
\begin{pmatrix}
1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 \\
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
1 & 1 \\
1 & 2 \\
1 & 3 \\
\end{pmatrix}
=
\begin{pmatrix}
4 & 6 \\
6 & 14 \\
\end{pmatrix}\\
A^TY=&
\begin{pmatrix}
1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 \\
\end{pmatrix}
\begin{pmatrix}1\\1\\2\\2\end{pmatrix}=
\begin{pmatrix}6\\11\end{pmatrix}
\end{align*}
$\left(\begin{array}{cc|c}
4 & 6 & 6 \\
6 &14 & 11
\end{array}\right)\sim$ $
\left(\begin{array}{cc|c}
2 & 3 & 3 \\
0 & 5 & 2
\end{array}\right)\sim$ $
\left(\begin{array}{cc|c}
2 & 0 & \frac95 \\
0 & 1 & \frac25
\end{array}\right)\sim$ $
\left(\begin{array}{cc|c}
1 & 0 & \frac9{10} \\
0 & 1 & \frac25
\end{array}\right)
$
Môžeme sa na to pozerať ako na približné riešenie sústavy:
\begin{align*}
\begin{pmatrix}
1 & x_1 \\
1 & x_2 \\
1 & x_3 \\
1 & x_4 \\
\end{pmatrix}
\begin{pmatrix}\beta_0\\\beta_1\end{pmatrix}=
\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}\\
\begin{pmatrix}
1 & 0 \\
1 & 1 \\
1 & 2 \\
1 & 3 \\
\end{pmatrix}
\begin{pmatrix}\beta_0\\\beta_1\end{pmatrix}=
\begin{pmatrix}1\\1\\2\\2\end{pmatrix}
\end{align*}
Opäť môžeme postupovať cez riešenie sústavy $A^TAB=A^TY$.
\begin{align*}
A^TA=&
\begin{pmatrix}
1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 \\
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
1 & 1 \\
1 & 2 \\
1 & 3 \\
\end{pmatrix}
=
\begin{pmatrix}
4 & 6 \\
6 & 14 \\
\end{pmatrix}\\
A^TY=&
\begin{pmatrix}
1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 \\
\end{pmatrix}
\begin{pmatrix}1\\1\\2\\2\end{pmatrix}=
\begin{pmatrix}6\\11\end{pmatrix}
\end{align*}
$\left(\begin{array}{cc|c}
4 & 6 & 6 \\
6 &14 & 11
\end{array}\right)\sim$ $
\left(\begin{array}{cc|c}
2 & 3 & 3 \\
0 & 5 & 2
\end{array}\right)\sim$ $
\left(\begin{array}{cc|c}
2 & 0 & \frac95 \\
0 & 1 & \frac25
\end{array}\right)\sim$ $
\left(\begin{array}{cc|c}
1 & 0 & \frac9{10} \\
0 & 1 & \frac25
\end{array}\right)
$
-
Martin Sleziak
- Posts: 5832
- Joined: Mon Jan 02, 2012 5:25 pm
Re: Aproximácia lineárnou funkciou (metóda najmenších štvorcov)
Derivovaním$\newcommand{\vek}[1]{\vec{#1}}
\newcommand{\skal}[2]{\langle{\vek{#1}},{\vek{#2}}\rangle}
\newcommand{\skl}[2]{\langle{#1},{#2}\rangle}
\newcommand{\abs}[1]{|{#1}|}$
Opäť skúsime použiť to, že nutnou podmienkou pre minimum sú nulové parciálne derivácie: viewtopic.php?t=1428
Ak chceme minimalizovať funkciu $g(\beta_0,\beta_1)=\sum\limits_{i=1}^n (\beta_0+\beta_1x_i-y_i)^2$, tak ako parciálne derivácie dostaneme
\begin{align*}
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_0} &= \sum\limits_{i=1}^n 2(\beta_0+\beta_1x_i-y_i)\\
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_1} &= \sum\limits_{i=1}^n 2x_i(\beta_0+\beta_1x_i-y_i)
\end{align*}
Ak položíme parciálne derivácie a trochu tieto rovnosti upravíme dostaneme
\begin{align}
\beta_0n + \beta_1 \sum_{i=1}^n x_i &= \sum_{i=1}^n y_i \tag{1}\\
\beta_0\sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2 &= \sum_{i=1}^n x_iy_i \tag{2}
\end{align}
To isté zapísané inak: Minimalizujem $g(\beta_0,\beta_1)=\abs{\beta_0\vek e+\beta_1\vek x-\vek y}^2=\skl{\beta_0\vek e+\beta_1\vek x-\vek y}{\beta_0\vek e+\beta_1\vek x-\vek y}$, kde $\vek e=(1,1,\dots,1)$. Teda
\begin{align*}
g(\beta_0,\beta_1)&=\beta_0^2 \abs{\vek e}^2 + \beta_1^2 \abs{\vek x}^2 + 2\beta_0\beta_1 \skal ex - \beta_0\skal ey - \beta_1 \skal xy + \abs{\vek y}^2\\
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_0} &= 2\beta_0 \abs{\vek e}^2 + 2\beta_1 \skal ex - \skal ey = 0 \\
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_1} &= 2\beta_0 \skal ex + 2\beta_1 \abs{\vek x}^2 - \skal xy = 0
\end{align*}
Ak do $(1)$ a $(2)$ dosadíme zadané hodnoty, tak v našom prípade dostaneme
\begin{align*}
4\beta_0+6\beta_1&=6\\
6\beta_0+14\beta_1&=11
\end{align*}
To je presne tá istá sústava, ktorú sme dostali v predošlom riešení.
\newcommand{\skal}[2]{\langle{\vek{#1}},{\vek{#2}}\rangle}
\newcommand{\skl}[2]{\langle{#1},{#2}\rangle}
\newcommand{\abs}[1]{|{#1}|}$
Opäť skúsime použiť to, že nutnou podmienkou pre minimum sú nulové parciálne derivácie: viewtopic.php?t=1428
Ak chceme minimalizovať funkciu $g(\beta_0,\beta_1)=\sum\limits_{i=1}^n (\beta_0+\beta_1x_i-y_i)^2$, tak ako parciálne derivácie dostaneme
\begin{align*}
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_0} &= \sum\limits_{i=1}^n 2(\beta_0+\beta_1x_i-y_i)\\
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_1} &= \sum\limits_{i=1}^n 2x_i(\beta_0+\beta_1x_i-y_i)
\end{align*}
Ak položíme parciálne derivácie a trochu tieto rovnosti upravíme dostaneme
\begin{align}
\beta_0n + \beta_1 \sum_{i=1}^n x_i &= \sum_{i=1}^n y_i \tag{1}\\
\beta_0\sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2 &= \sum_{i=1}^n x_iy_i \tag{2}
\end{align}
To isté zapísané inak: Minimalizujem $g(\beta_0,\beta_1)=\abs{\beta_0\vek e+\beta_1\vek x-\vek y}^2=\skl{\beta_0\vek e+\beta_1\vek x-\vek y}{\beta_0\vek e+\beta_1\vek x-\vek y}$, kde $\vek e=(1,1,\dots,1)$. Teda
\begin{align*}
g(\beta_0,\beta_1)&=\beta_0^2 \abs{\vek e}^2 + \beta_1^2 \abs{\vek x}^2 + 2\beta_0\beta_1 \skal ex - \beta_0\skal ey - \beta_1 \skal xy + \abs{\vek y}^2\\
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_0} &= 2\beta_0 \abs{\vek e}^2 + 2\beta_1 \skal ex - \skal ey = 0 \\
\frac{\partial g(\beta_0,\beta_1)}{\partial \beta_1} &= 2\beta_0 \skal ex + 2\beta_1 \abs{\vek x}^2 - \skal xy = 0
\end{align*}
Ak do $(1)$ a $(2)$ dosadíme zadané hodnoty, tak v našom prípade dostaneme
\begin{align*}
4\beta_0+6\beta_1&=6\\
6\beta_0+14\beta_1&=11
\end{align*}
To je presne tá istá sústava, ktorú sme dostali v predošlom riešení.
-
Martin Sleziak
- Posts: 5832
- Joined: Mon Jan 02, 2012 5:25 pm
Re: Aproximácia lineárnou funkciou (metóda najmenších štvorcov)
Čo nám vlastne vyšlo
Vlastne sme dostali, že lineárna funkcia, ktorá najlepšie (v zmysle najmenších štvorcov) aproximuje zadané dáta je
$$y=\frac9{10}+\frac4{10}x.$$
Na tomto obrázku vidíme zadané body a lineárnu funkciu, ktorá nám vyšla.
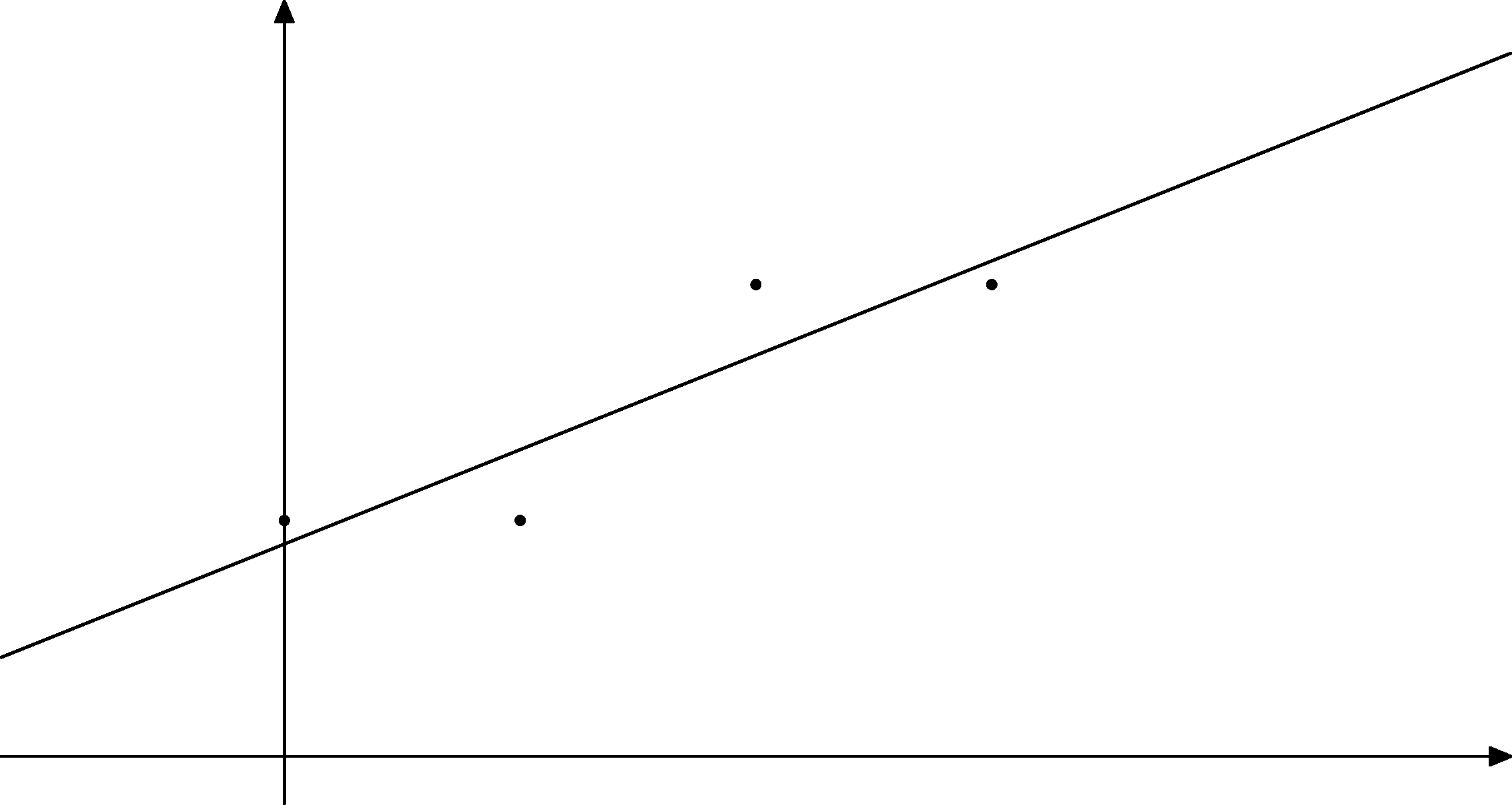
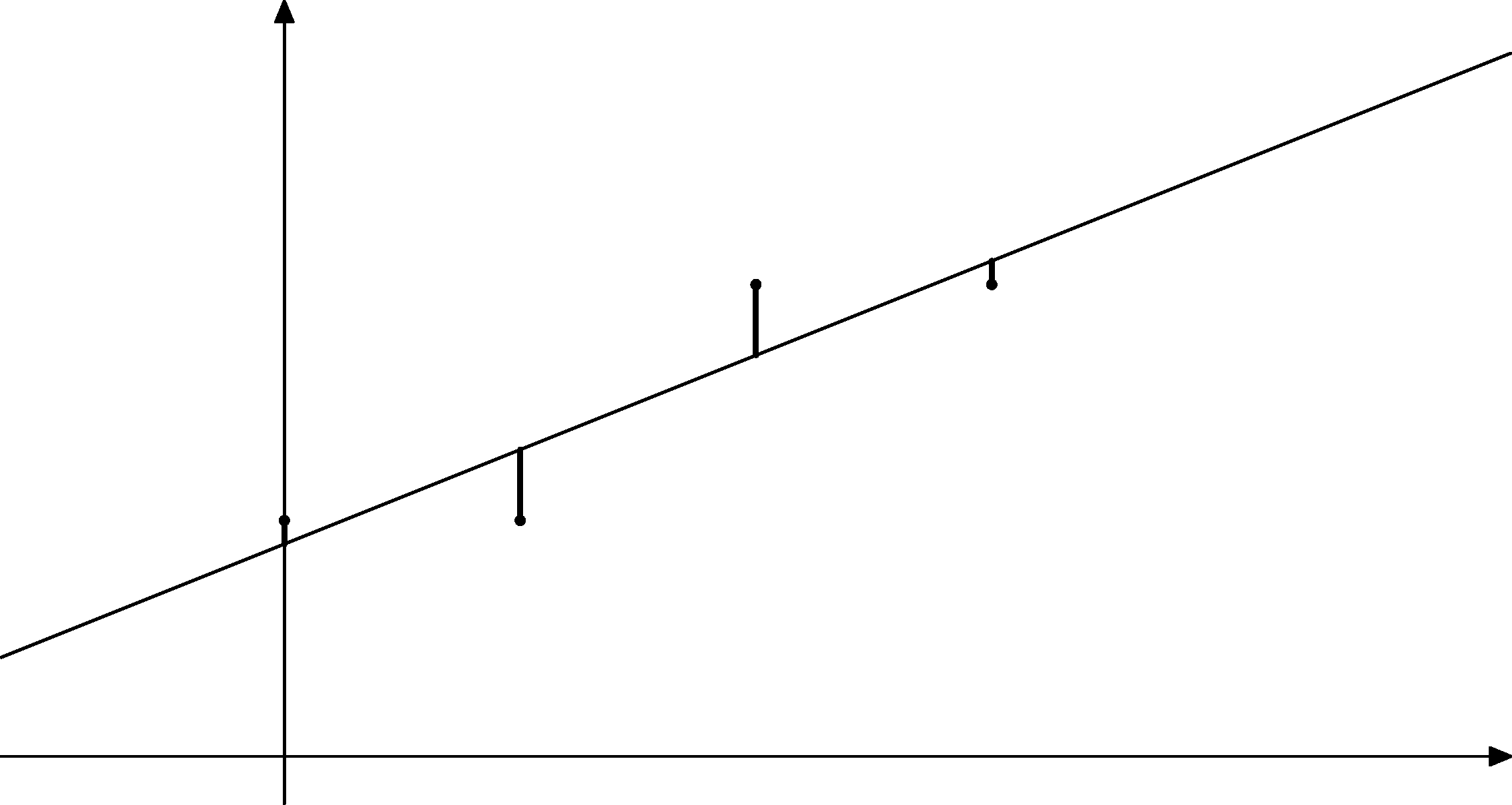
Tu sú vyznačené aj úsečky, pre ktoré sme minimalizovali súčet štvorcov.
Vlastne sme dostali, že lineárna funkcia, ktorá najlepšie (v zmysle najmenších štvorcov) aproximuje zadané dáta je
$$y=\frac9{10}+\frac4{10}x.$$
Na tomto obrázku vidíme zadané body a lineárnu funkciu, ktorá nám vyšla.

Tu sú vyznačené aj úsečky, pre ktoré sme minimalizovali súčet štvorcov.
