Z $f^3=f^2$ nevyplýva $f^2=f$

[Martin Sleziak]

Už som na fórum napísal niečo k tomu, že takáto implikácia platí ak $f$ je injektívne alebo surjektívne: https://msleziak.com/forum/viewtopic.php?t=1723

Zostala nám už iba úloha z jednej skupiny. Tu už nedávame žiadne dodatočné podmienky, o $f$ vieme iba to, že to je zobrazenie z $M$ do $M$.
Z prípadov, na ktoré som sa pýtal, toto je jediný, kde tvrdenie neplatí. A teda tu by sme chceli nájsť kontrapríklad.

Nech $M\ne\emptyset$ je množina a $f\colon M\to M$ je zobrazenie. Ak platí $f\circ f\circ f=f\circ f$, tak platí aj $f\circ f=f$.

Ak vieme všetky tvrdenia, ktoré sme uviedli vyššie, tak je jasné, že ak nájdeme nejaký kontrapríklad, tak $f$ nemôže byť ani injekcia ani surjekcia.

Skúsme vymyslieť čo najjednoduchší príklad zobrazenia $f\colon M\to M$, ktoré nie je ani injektívne ani surjektívne. (Síce takéto zobrazenie nepovedie k tomu, čo chceme dostať. Ale napíšem ho sem v nádeji, že keď niekto chvíľu bude pozerať na takýto príklad, tak už má šancu prísť aj na taký, ktorý naozaj funguje.)

Asi je vcelku ľahké prísť na to, že potrebujeme aspoň dvojprvkovú množinu $M$.
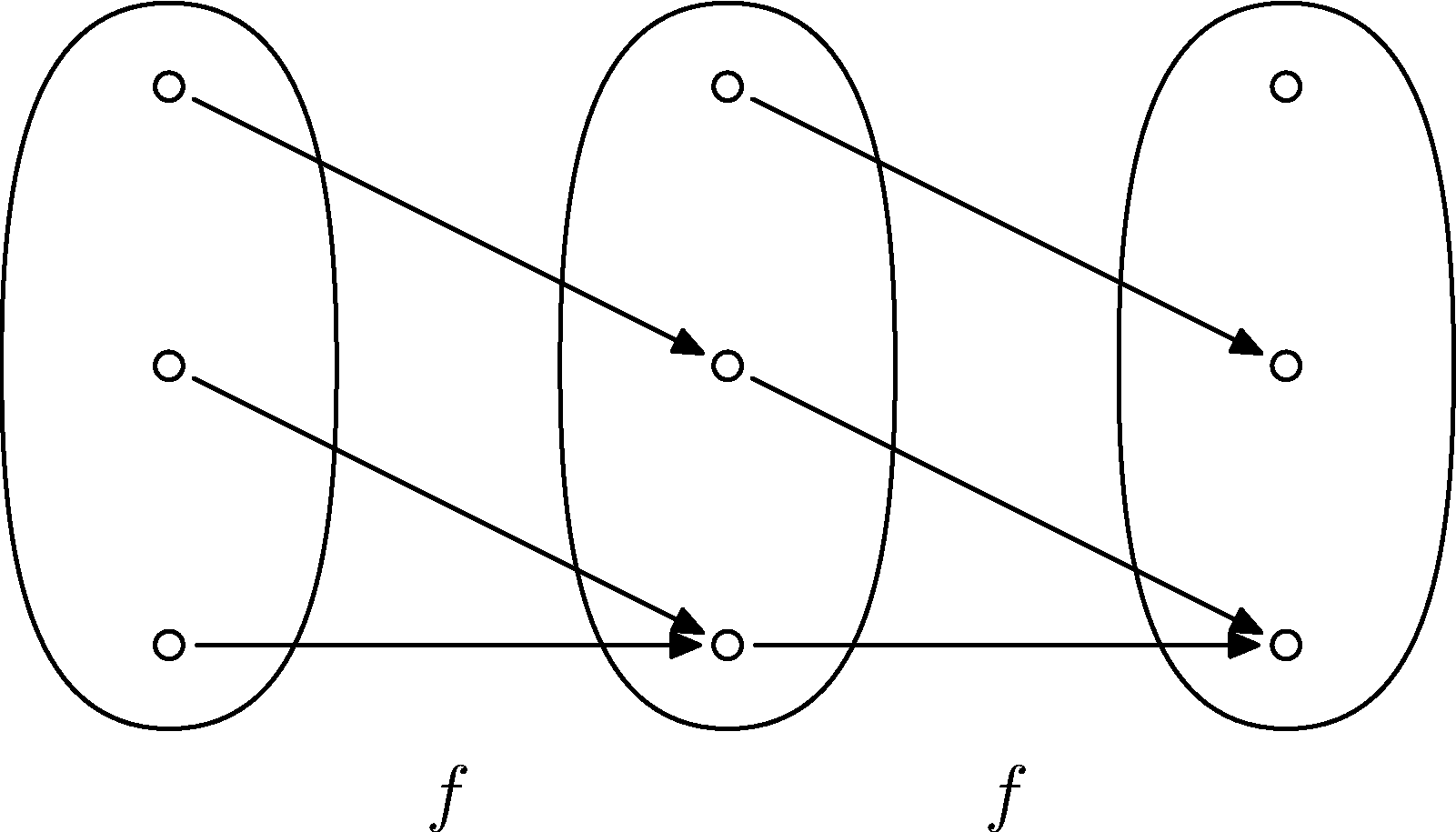
Môžeme napríklad zobrať $M=\{0,1\}$. Potom zobrazenie určené tým, že $f(0)=f(1)=0$ je príklad zobrazenia $M\to M$, ktoré nie je ani injektívne ani surjektívne.
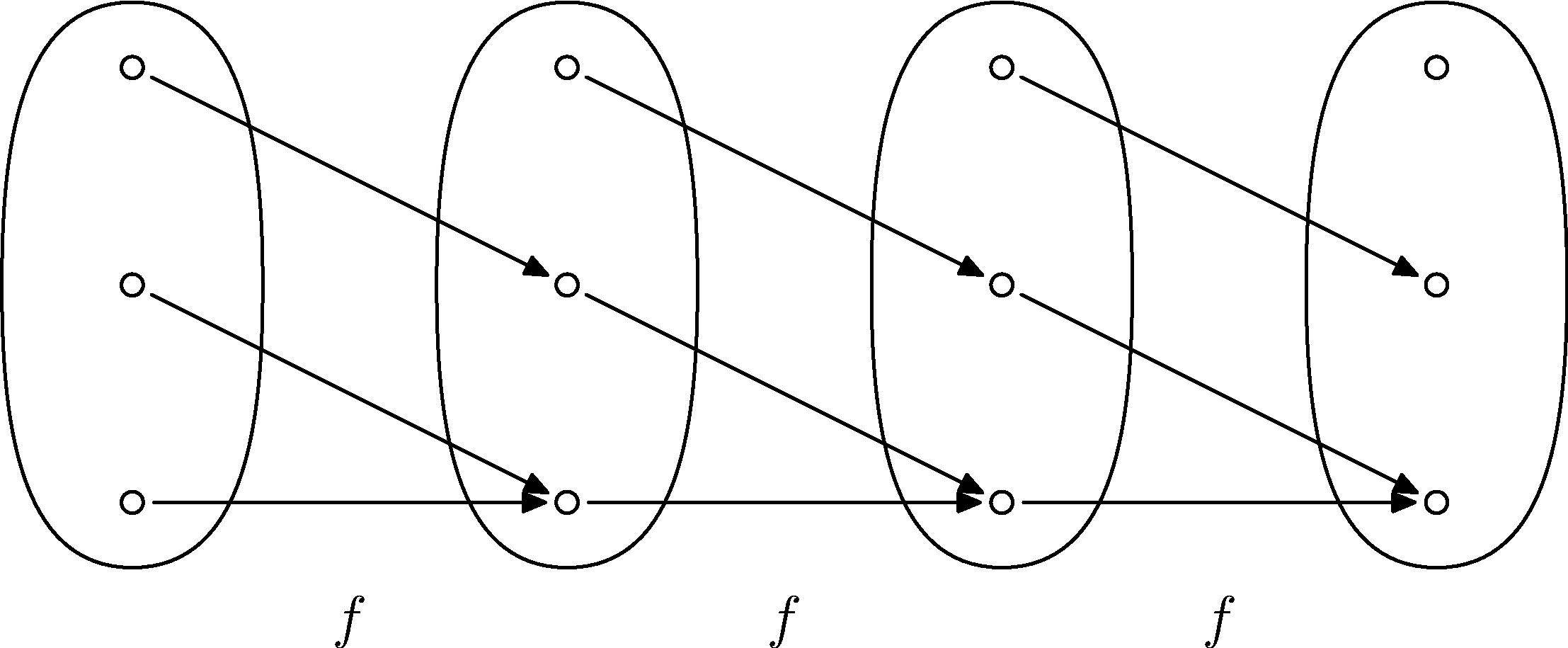
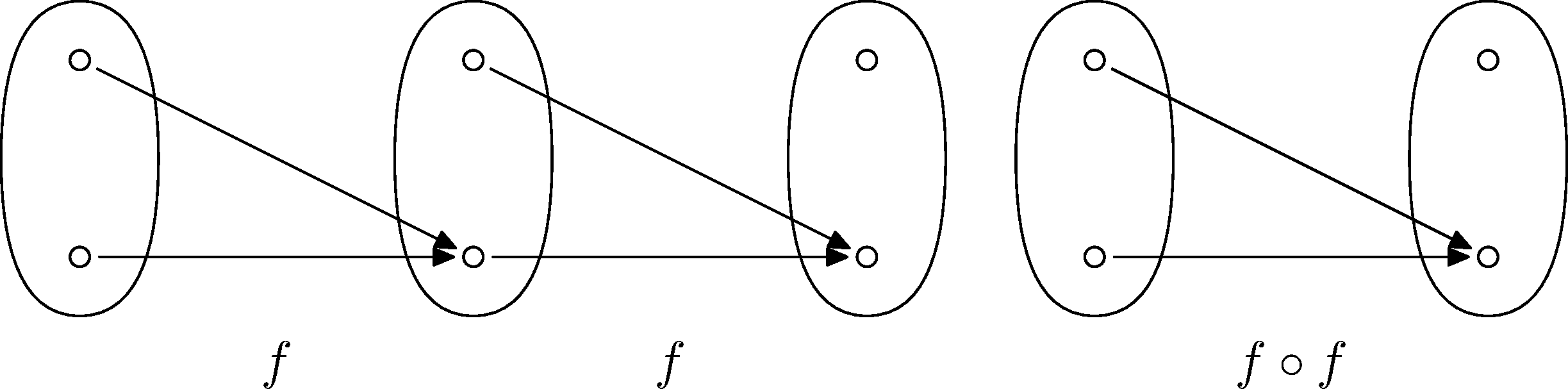
Poďme sa pozrieť na to, čo v tomto prípade dostaneme, ak vypočítame $f\circ f$ a $f\circ f\circ f$.

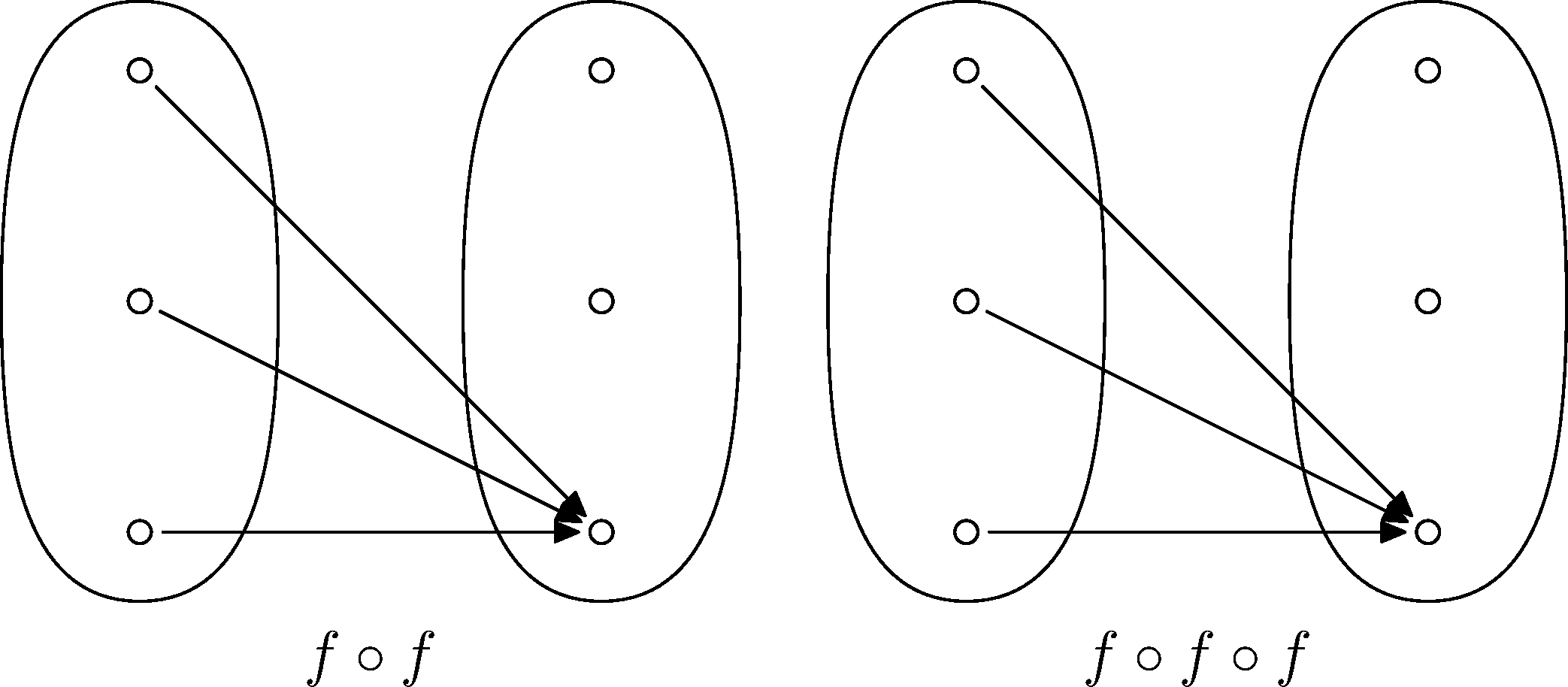
Toto dostaneme, ak túto funkciu zložíme dvakrát:


A takto vyzerá trojnásobné zloženie:


Teda toto nie je celkom taký príklad ako chceme. Dostali sme $f\circ f\circ f=f\circ f=f$. (A nie je ťažké si uvedomiť, že to isté platí pre ľubovoľnú množinu $M$ a ľubovoľné konštantné zobrazenie.)

My však chceme nájsť príklad taký, že platí $f\circ f\circ f=f\circ f$ a súčasne $f\circ f\ne f$.

Budeme potrebovať aspoň trojprvkovú množinu $M$.

Súčasne sme si uvedomili, že ak chceme nájsť takéto $M$, tak:

• $f$ nesmie byť konštantné zobrazenie;
• $f$ nesmie byť injektívne zobrazenie;
• $f$ nesmie byť surjektívne zobrazenie.

Vyzbrojený týmito vedomosťami by ste sa mohli skúsiť zamyslieť nad tým, či teraz už taký príklad nevymyslíte. Alebo si nejaký taký príklad môžete pozrieť nižšie.

Spoiler:

Môžeme zobrať $M=\{0,1,2\}$ a funkciu $f\colon M\to M$ definovanú ako $f(0)=f(1)=0$, $f(2)=f(1)$.
Zložením spočítame, že $f\circ f$ aj $f\circ f\circ f$ je konštantná funkcia, ktorá každý prvok z $M$ zobrazí na nulu.
Teda pre túto funkciou máme $$f\circ f\circ f = f\circ f \qquad\text{a}\qquad f\circ f\ne f.$$
(Aby sme videli, že $f\circ f$ a $f$ sú navzájom rôzne funkcie, stačí si všimnúť, že $f(f(2))=0$ a $f(2)=1$, t.j. $(f\circ f)(2)\ne f(2)$.)

Ak to pomôže, môžete si túto funkciu $f$ (a aj funkcie $f\circ f$ a $f\circ f\circ f$) skúsiť nakresliť, aby ste videli, ako to tu vychádza. Nejaké obrázky si môžete pozrieť tu:

Spoiler:

Takto vyzerá funkcia $f$:


Štandardným spôsobom vieme zistiť ako vyzerá zložená funkcia $f\circ f$:


A ak pridáme ešte jedno zloženie z $f$, tak dostaneme niečo takéto


Ak porovnáme výsledky, v oboch prípadoch vyšla tá istá (konštantná) funkcia:

[Martin Sleziak]

Napíšem sem aj jedno z odovzdaných riešení - ktoré bolo vcelku pekné.

Definujme zobrazenie $f\colon\mathbb Z\to\mathbb Z$ tak, že
$$f(x)=
\begin{cases}
0 & \text{ak }2\mid x, \\
x+1 & \text{ak }2\nmid x.
\end{cases}
$$
T.j. zobrazenie $f$ posiela párne čísla na nulu a nepárne posúva o $1$.

Pozrime sa, ako vyzerá $f\circ f$ a $f\circ f\circ f$.

Prídeme na to, že pre všetky $x\in\mathbb Z$ platí $$f\circ f(x)=0.$$

a) Ak $x$ je párne, tak $f(x)=0$ a aj $f(f(x))=f(0)=0$.
b) Ak $x$ je nepárne, tak $f(x)=x+1$ je párne a $f(f(x))=f(x+1)=0$.

A dostaneme aj $$f(f(f(x)))=0$$ pre každé $x\in\mathbb Z$; tu už stačí využiť, že $f(f(f(x)))=f(0)=0$.

Teda je to skutočne príklad funkcie takej, že $f\circ f\circ f=f\circ f$ a súčasne $f\circ f\ne f$.

Poznamenám, že sa dá zbadať nejaká podobnosť na príklad, ktorý sme spomenuli vyššie. Ak sa pozriete na čísla $0$, $1$ a $2$ (t.j. na zúženie na množinu $\{0,1,2\}$), tak vidíte, že $0\mapsto 0$, $2\mapsto 0$, $1\mapsto 2$. Ak si v obrázku, ktorý sme nakreslili vyššie, body vhodne označíte ako $0$, $1$, $2$, tak dostanete presne takéto zobrazenie.

[Martin Sleziak]

Komentáre k odovzdaným riešeniam

Na to, aby sme zdôvodnili, že dve zobrazenia sú rôzne, stačí nájsť jeden bod v definičnom obore, kde sa funkčné hodnoty líšia.

Niektorí ste v riešení našli $\operatorname{Im}(f)$ a $\operatorname{Im}(f\circ f)$ a z $\operatorname{Im}(f)\ne \operatorname{Im}(f\circ f)$ ste dospeli k záveru, že $f\ne f\circ f$. Takýto argument je tiež úplne v poriadku.

Ale takýto zápis nie je správny:

$f=\{0,1\}$
$f\circ f=\{0\}$

Aj keď som pochopil, že ste mali na mysli $\operatorname{In}(f)=\{0,1\}$ a $\operatorname{In}(f\circ f)=\{0\}$.