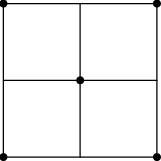
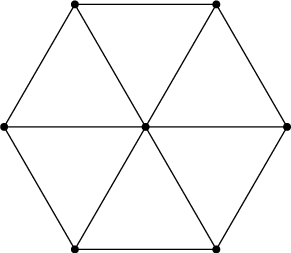
Riešenie.V pravidelnom šesťuholníku so stranou dĺžky $1$ je rozmiestnených sedem bodov. Ukážte, že niektoré dva z nich majú vzdialenosť najviac $1$.
Stačí rozdeliť šesťuholník na 6 rovnostranných trojuholníkov so stranou 1. V niektorom z nich sa musia podľa holubníkového princípu nachádzať dva body. Maximálna vzdialenosť bodov v malom trojuholníku je 1 (stačí skontrolovať, aké sú vzdialenosti medzi vrcholmi).
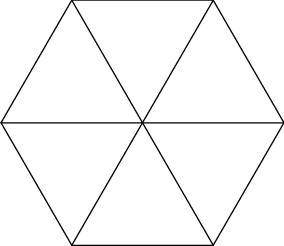
Riešenie.Dokážte: Ak máme päť bodov vo štvorci so stranou $2$, tak sa medzi nimi dajú nájsť dva rôzne body, ktorých vzdialenosť je nanajvýš $\sqrt2$.
Stačí rozdeliť štvorec na 4 menšie štvorce s hranou 1. V niektorom z nich sa musia podľa holubníkového princípu nachádzať dva body. Maximálna vzdialenosť bodov v malom štvorci je 1 (stačí skontrolovať, aké sú vzdialenosti medzi vrcholmi).
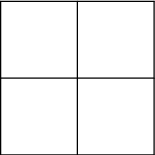
Iné riešenie pre štvorec. Našlo sa v jednej písomke riešenie, ktoré sa zhruba dá preformulovať takto:
Štvrťkruhy s polomermi $\sqrt2$ a vrcholmi vo vrcholoch štvorca pokryjú celý štvorec Podľa holubníkového princípu v niektorom z nich musia byť dva body. Maximálna vzdialenosť bodov v štvrťkruhu je $\sqrt2$.
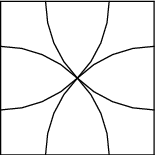
Takéto riešenie je ok. Aj keď vidieť aká je maximálna vzdialenosť pre body v štvrťkruhu nie je na prvý pohľad také zrejmé, ako keď sme to rozdelili na štvorce.
Poznámka. Aká je maximálna vzdialenosť medzi bodmi menších častí ("krabičiek") sa dá zdôvodniť rozličnými spôsobmi. V tomto prípade ide o $n$-uholníky, tu nám stačí skontrolovať vzájomné vzdialenosti pre všetky dvojice vrcholov. (Aj keď toto by sa tiež asi patrilo zdôvodniť.) Ale v riešeniach na písomke som bol úplne spokojný s tým, keď ste napísali maximálnu vzdialenosť bez akéhokoľvek zdôvodnenia. (Za predpokladu, že bola správna.)