Jedna z úloh síce nie je presne rovnaká, ale je podobná na staršiu úlohu, ktorá sa dá nájsť tu: viewtopic.php?t=1361
Aspoň niečo k zostávajúcej úlohe. (Ak by bolo niečo nejasné, tak sa určite nebojte spýtať - či už na konzultáciách alebo tu na fóre. Takisto ak máte iné riešenia úloh, môžete sa nimi pochváliť. Alebo ak máte nejaký nápad ako riešiť niektorú časť iným spôsobom, tak sa tu môžete opýtať či by to tak išlo.)$\newcommand{\R}{\mathbb R}
\newcommand{\Ker}{\operatorname{Ker}}
\newcommand{\Ima}{\operatorname{Im}}$
Zadanie.
Druhá skupina mala veľmi podobné zadanie - boli tam iné čísla, všetky podstatné veci tam vyjdú rovnako resp. veľmi podobne. (Konkrétne tam bolo $f(x,y)=(4x-2y,2x-y)$.)Uvažujte zobrazenie $f\colon (\R^2,+) \to (\R^2,+)$ dané nasledovne:
$$f(x,y)=(3x-2y,6x-4y).$$
a) Ukážte, že toto zobrazenie je homomorfizmus grúp.
b) Určte $\Ker(f)$ a $\Ima(f)$.
c) Je $f$ injektívne? Je $f$ surjektívne?
d) S akou známou grupou je faktorová grupa $\R^2/\Ker(f)$ izomorfná?
Riešenie.
Je to homomorfizmus.
Máme vlastne overiť, či pre ľubovoľné $(x_1,y_1),(x_2,y_2)\in\R^2$ platí
$$f(x_1,y_1)+f(x_2,y_2)=f(x_1+x_2,y_1+y_2).$$
Toto sa dá skontrolovať pomerne ľahko priamo z definície zobrazenia $f$.
Spoiler:
Už teda vieme, že $f$ je homomorfizmus. Chceme nájsť jeho jadro a obraz.
Jadro sú tie prvky z $\mathbb R^2$, ktoré sa zobrazia na $(0,0)$. Teda vlastne dostávame dve podmienky:
\begin{align*}
3x-2y&=0\\
6x-4y&=0
\end{align*}
Vidno však, že druhá rovnica je presne dvojnásobkom prvej. Teda akonáhle je splnená prvá rovnica, tak platí aj druhá. Čiže tieto dve podmienky môžeme nahradiť jednou a vidíme, že
$$\Ker f=\{(x,y)\in\mathbb R^2; 3x-2y=0\}.$$
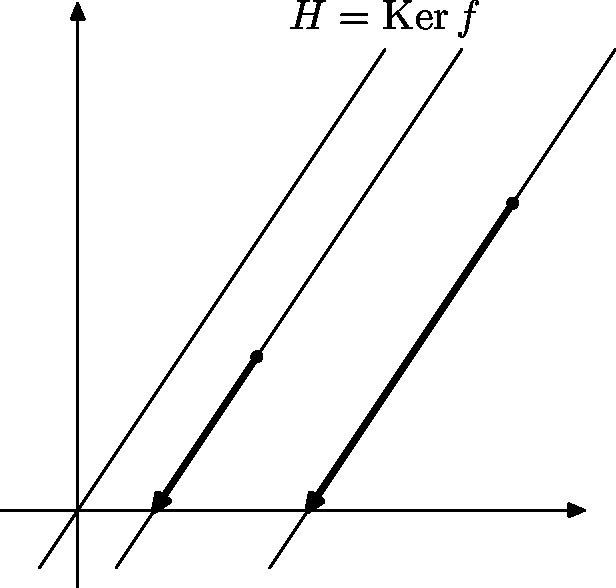
Môžeme si všimnúť, že $\Ker f$ je vlastne priamka prechádzajúca nulou s normálovým vektorom $(3,-2)$. (Vieme takúto množinu bodov aj načrtnúť. Máme túto priamku zapísanú pomocou všeobecnej rovnice - zo strednej školy vieme, že pre ľubovoľné konštanty $a,b,c\in\R$ množina bodov určená rovnicou $ax+by+c=0$ predstavuje priamku.)
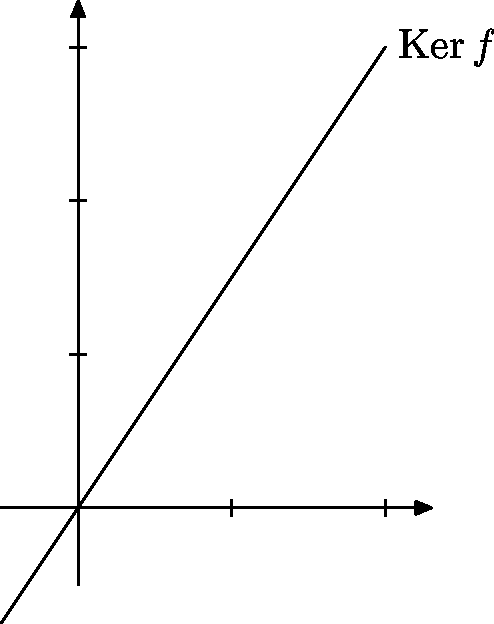
Chceme nájsť aj obraz $f$. T.j. chceme zistiť ktoré prvky sa dajú dostať ako $f(x,y)$ pre nejaké $x,y\in\R$.
Keď sa pozrieme na predpis $f(x,y)=(3x-2y,6x-4y)$, tak hneď vidíme, že druhá súradnica je dvojnásobkom druhej.
Dostaneme teda iba body tvaru $(t,2t)$. (Kde $t$ je nejaké reálne číslo.)
Dá sa dostať každý takýto bod ako obraz nejakého $(x,y)$?
Nie je ťažké nájsť pre zadané $t\in\R$ aspoň jeden vzor pre $(t,2t)$.
Spoiler:
Opäť si môžeme všimnúť, že sme dostali priamku prechádzajúcu nulou. (Tentokrát je zapísaná pomocou parametrického vyjadrenia. Z neho vidíme, že smerový vektor je $(1,2)$.)
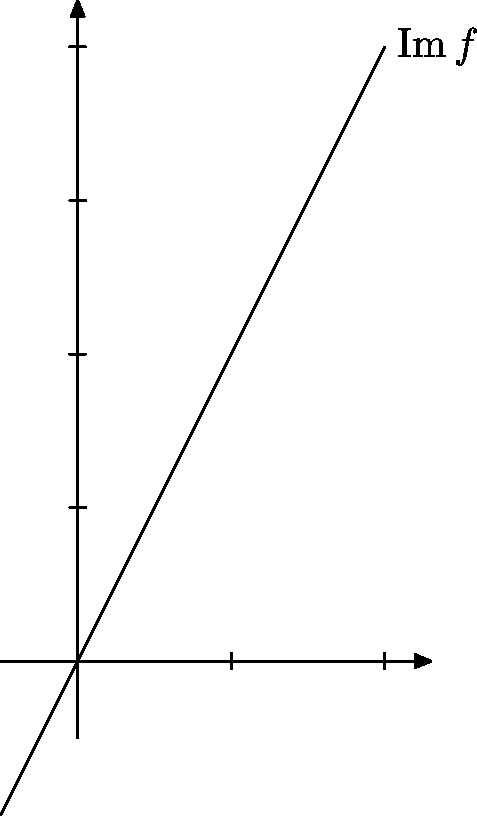
Môžeme si pripomenúť, že z prednášky vieme, že $\Ker f$ aj $\Ima f$ sú podgrupy. (Platí to pre každý homomorfizmus, teda aj v našom prípade. Aj keď tu sú obe podgrupy dosť jednoduché na to, že to vidno ľahko i z kritéria podgrupy.)
Injektívnosť, surjektívnosť.
Vieme, že pre homomorfizmus $f\colon G\to G'$ platí, že
- $f$ je injektívny $\Leftrightarrow$ $\Ker f=\{e_G\}$;
- $f$ je surjektívny $\Leftrightarrow$ $\Ima f=G'$.
Takisto existujú prvky z $\R^2$, ktoré nepatria do $\Ima f$, čiže dostávame, že $f$ nie je epimorfizmus.
Ak by sme to isté chceli zdôvodniť bez odvolávanie sa na uvedenú vetu, čiže priamo z definície, tak si napríklad stačí všimnúť, že:
- $f(0,0)=0=f(2,3)$, teda sme našli dva rôzne body $(0,0)\ne(2,3)$, ktoré sa zobrazia na to isté (a teda $f$ nie je injektívne);
- Bod $(1,1)$ nie je tvaru $(t,2t)$ pre žiadne $t\in\R$, naň sa teda nezobrazí nič (čiže $f$ nie je surjektívne).
Faktorová grupa.
Pripomeňme, čo vieme z vety o faktorovom izomorfizme:
V našom prípade dostaneme $\R^2/\Ker f\cong\{(t,2t); t\in\R\}$, pričom na uvedenú priamku sa pozeráme ako na podgrupu grupy $(\R^2,+)$. (T.j. operáciu $+$ chápeme ako sčitovanie po súradniciach.)Ak $G$ je komutatívna grupa a $f\colon G\to G'$ je grupový homomorfizmus, tak $\Ker f$ je podgrupa grupy $G$ a pre faktorovú grupu platí
$$G/\Ker f\cong \Ima f.$$
(Ak homomorfizmus $f$ je navyše surjektívny, tak priamo dostaneme $G/\Ker f\cong G'$.)
Označme si túto podgrupu ako $(G',+)$, t.j. $G'=\Ima f=\{(t,2t); t\in\R\}$.
V zadaní máme otázku s akou známou grupou je táto faktorová grupa izomorfná. Čiže sa tu asi čaká niečo také, že by sme mali nájsť nejakú grupu izomorfnú s $\R^2/\Ker f$ medzi základnými príkladmi grúp, ktoré sme kedysi videli.
Už ale vieme, že to je to isté ako hľadať grupu izomorfnú s $G'$ (keďže $G'$ a $\R^2/\Ker f$ sú izomorfné).
Nie je ťažké si uvedomiť, že zobrazenie $g\colon \R \to G'$ definované ako
$$g(t)=(t,2t)$$
je bijekcia medzi $\R$ a priamkou $G'$. A dá sa skontrolovať aj to, že je to homomorfizmus $(\R,+)\to(G',+)$, keďže máme
$$g(t+t')=(t+t',2(t+t'))=(t,2t)+(t',2t')=g(t)+g(t').$$
(Akonáhle sme overili, že $g$ je izomorfizmus, tak na kontrolu injektívnosti/surjektívnosti $g$ môžeme použiť jadro/obraz, podobne ako sme to urobili s homomorfizmom $f$ zo zadania.)
Vidíme teda, že $G'$ je izomorfná s $(\R,+)$.
To znamená, že aj faktorová grupa $\R^2/\Ker f$ je izomorfná s $(\R,+)$.