Zadania$\newcommand{\Zobr}[3]{#1\colon#2\to#3}\newcommand{\inv}[1]{#1^{-1}}$
Skupina A: Dokážte, alebo nájdite kontrapríklad: Ak $\Zobr fXX$ je zobrazenie také, že $f\circ f=id_X$, tak $f=id_X$.
Skupina B: Dokážte, alebo nájdite kontrapríklad: Ak $\Zobr fXX$ je zobrazenie také, že $f\circ f=f$, tak $f=id_X$.
Skupina C: Dokážte, alebo nájdite kontrapríklad: Ak $\Zobr{f,g}XX$ sú zobrazenia také, že $g\circ f=id_X$, tak $g=id_X$.
Skupina D: Dokážte, alebo nájdite kontrapríklad: Ak $\Zobr{f,g}XX$ sú zobrazenia také, že $g\circ f=id_X$, tak $g$ je injektívne.
Vo fóre k inému predmetu sa dajú nájsť veľmi podobné úlohy - tam bolo zadanie také, že treba hľadať príklady pre $X=\mathbb N$. (Táto požiadavka však obtiažnosť úlohy nejako diametrálne nemení.)
Nejaké príklady z minulých rokov z podobných tém sa dajú nájsť tu:
viewtopic.php?t=1467
viewtopic.php?t=1325
viewtopic.php?t=735
viewtopic.php?t=493
Tu je staršia písomka, kde sú tri z týchto štyroch príkladov: viewtopic.php?t=1153
Kontrapríklady na skladanie funkcií
Moderators: Martin Sleziak, Ludovit_Balko, Martin Niepel, Tibor Macko
-
Martin Sleziak
- Posts: 5689
- Joined: Mon Jan 02, 2012 5:25 pm
Re: Kontrapríklady na skladanie funkcií
Riešenia:$\newcommand{\Zobr}[3]{#1\colon#2\to#3}\newcommand{\inv}[1]{#1^{-1}}$
Vo všetkých skupinách sa dá nájsť kontrapríklad, ktorý ukazuje, že zadané tvrdenie neplatí.
Skupina A:
Jednoduchým kontrapríkladom je zobrať konštantnú funkciu, pričom $X$ je aspoň dvojprvková množina.
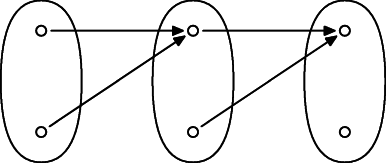
Skupina B:
Podmienka $f\circ f=id_X$ nám hovorí, že $f=\inv f$. A z toho vlastne vidno, že pre každý prvok buď platí $f(x)=x$, alebo funkcia navzájom vymieňa dvojice prvkov. T.j. ak máme $f(x)=y$, tak musí platiť aj obrátene $f(y)=x$.
Keď sme si uvedomili toto, tak už nie je ťažké nájsť kontrapríklad. Môžeme zobrať napríklad $X=\{0,1\}$ a zobrazenie definované ako $f(0)=1$ a $f(1)=0$. (T.j. zobrazenie, ktoré vymieňa nulu a jednotku.)
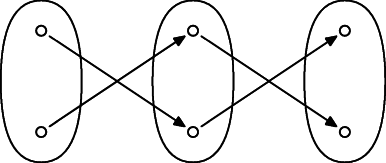
Aj iné príklady budú obsahovať takéto dvojice prvkov. Napríklad $\Zobr f{\mathbb R}{\mathbb R}$ definované ako $f(x)=-x$.
Zobrazenia s vlastnosťou $f\circ f=id_X$ (t.j. $f=\inv f$) sa volajú involúcie.
Skupina C:
Akýkoľvek kontrapríklad zo skupiny B funguje aj tu. Akýkoľvek kontrapríklad zo skupiny D funguje aj tu.
Skupina D:
Chceme nájsť príklad, kde $g$ nebude injektívne. Teda nejaké dva prvky sa musia zobrazením $g$ zobraziť na to isté. Celkom by sa nám núkal príklad ako na nasledujúcom obrázku - tam ale nesedí to, že chceme aby obor aj koobor bola pre $f$ aj $g$ tá istá množina $X$.
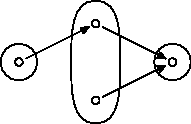
Keď však "pospájame" niečo podobné nekonečne veľakrát, tak sa nám podarí nájsť nejaký kontrapríklad. Môžeme zobrať napríklad $X=\{1,2,\dots,\}$ a zobrazenia určené tak, že $f(n)=2n$ a
$$g(n)=
\begin{cases}
k & \text{ak }n=2k, \\
k & \text{ak }n=2k-1.
\end{cases}
$$
Teda $f$ zobrazí každý prvok na jeho dvojnásobok. Zobrazenie $g$ zvolíme tak, že párne čísla zobrazuje "naspäť". A pre nepárne čísla si už potom môžeme zvoliť čokoľvek.
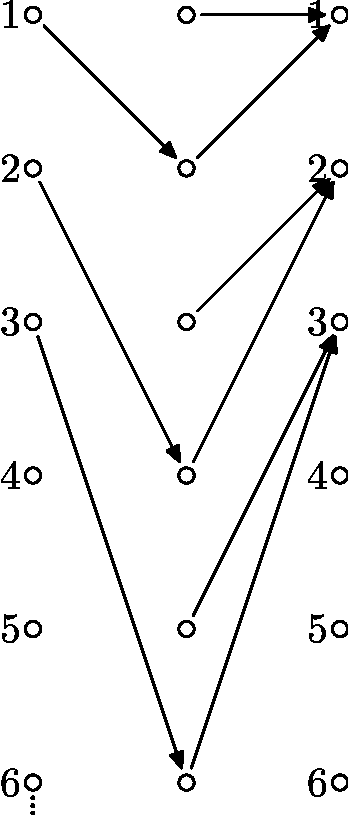
V súvislosti s touto úlohou sa oplatí spomenúť, že kontrapríklad kde by množina $X$ bola konečná sa nájsť nedá.
Ak $X$ je konečná množina, tak pre zobrazenie $\Zobr fXX$ sú injektívnosť, surjektívnosť a bijektívnosť ekvivalentné. (Napríklad úloha 1.4 v 01zobrazenia.pdf.)
Vo všetkých skupinách sa dá nájsť kontrapríklad, ktorý ukazuje, že zadané tvrdenie neplatí.
Skupina A:
Jednoduchým kontrapríkladom je zobrať konštantnú funkciu, pričom $X$ je aspoň dvojprvková množina.

Skupina B:
Podmienka $f\circ f=id_X$ nám hovorí, že $f=\inv f$. A z toho vlastne vidno, že pre každý prvok buď platí $f(x)=x$, alebo funkcia navzájom vymieňa dvojice prvkov. T.j. ak máme $f(x)=y$, tak musí platiť aj obrátene $f(y)=x$.
Keď sme si uvedomili toto, tak už nie je ťažké nájsť kontrapríklad. Môžeme zobrať napríklad $X=\{0,1\}$ a zobrazenie definované ako $f(0)=1$ a $f(1)=0$. (T.j. zobrazenie, ktoré vymieňa nulu a jednotku.)

Aj iné príklady budú obsahovať takéto dvojice prvkov. Napríklad $\Zobr f{\mathbb R}{\mathbb R}$ definované ako $f(x)=-x$.
Zobrazenia s vlastnosťou $f\circ f=id_X$ (t.j. $f=\inv f$) sa volajú involúcie.
Skupina C:
Akýkoľvek kontrapríklad zo skupiny B funguje aj tu. Akýkoľvek kontrapríklad zo skupiny D funguje aj tu.
Skupina D:
Chceme nájsť príklad, kde $g$ nebude injektívne. Teda nejaké dva prvky sa musia zobrazením $g$ zobraziť na to isté. Celkom by sa nám núkal príklad ako na nasledujúcom obrázku - tam ale nesedí to, že chceme aby obor aj koobor bola pre $f$ aj $g$ tá istá množina $X$.

Keď však "pospájame" niečo podobné nekonečne veľakrát, tak sa nám podarí nájsť nejaký kontrapríklad. Môžeme zobrať napríklad $X=\{1,2,\dots,\}$ a zobrazenia určené tak, že $f(n)=2n$ a
$$g(n)=
\begin{cases}
k & \text{ak }n=2k, \\
k & \text{ak }n=2k-1.
\end{cases}
$$
Teda $f$ zobrazí každý prvok na jeho dvojnásobok. Zobrazenie $g$ zvolíme tak, že párne čísla zobrazuje "naspäť". A pre nepárne čísla si už potom môžeme zvoliť čokoľvek.

V súvislosti s touto úlohou sa oplatí spomenúť, že kontrapríklad kde by množina $X$ bola konečná sa nájsť nedá.
Ak $X$ je konečná množina, tak pre zobrazenie $\Zobr fXX$ sú injektívnosť, surjektívnosť a bijektívnosť ekvivalentné. (Napríklad úloha 1.4 v 01zobrazenia.pdf.)
-
Martin Sleziak
- Posts: 5689
- Joined: Mon Jan 02, 2012 5:25 pm
Re: Kontrapríklady na skladanie funkcií
Komentáre k odovzdaným úlohám:$\newcommand{\Zobr}[3]{#1\colon#2\to#3}\newcommand{\inv}[1]{#1^{-1}}$
Skupina A: Tu upozorním, že aby ste úplne zadali funkciu, mali by ste aj povedať čomu sa rovná $X$. Niektorí ste napísali iba $f(x)=-x$ a nenapísali ste, s akou množinou robíte. (Napríklad pre $X=\mathbb R$ alebo $X=\mathbb Z$ funkcia $f(x)=-x$ funguje ako kontrapríklad. Ale ak napríklad $X=\{0\}$, tak to kontrapríklad nie je.)
Skupina B: Viacerí z vás napísali niečo také, že ak na obe strany rovnosti $f\circ f=f$ aplikujeme $\inv f$, tak dostaneme $f=id_X$. To je pravda - ale len za predpokladu že $\inv f$ existuje; takže takýto argument prejde pre bijektívne zobrazenie $f$. (A hovorí nám to teda, že ak chceme nájsť kontrapríklad, musíme použiť nejakú funkciu, ktorá nie je bijektívna.)
Skupina D: Niektorí z vás poslali riešenie, kde nešlo o zobrazenia z tej istej množiny do tej istej množiny. Napríklad niečo podobné ako na obrázku, ktorý som ukázal vyššie:

Keďže mi chceme aby $f$ aj $g$ boli zobrazenia $X\to X$, tento kontrapríklad je trochu iný ako to čo sa chce v zadaní.
Takisto som dostal riešenie, kde bolo odvodené, že $g$ je surjektívne. A potom bolo tvrdenie, že z toho už vyplýva aj injektívnosť $g$.
Ako vidno z príkladu vyššie, toto nie je pravda.
Bola by to pravda pre konečnú množinu $X$ a zobrazenie $\Zobr gXX$. (A aj riešenie, kde bolo takéto tvrdenie uvedené, sa nejako odvolávalo na počet prvkov množiny $X$.)
Skupina A: Tu upozorním, že aby ste úplne zadali funkciu, mali by ste aj povedať čomu sa rovná $X$. Niektorí ste napísali iba $f(x)=-x$ a nenapísali ste, s akou množinou robíte. (Napríklad pre $X=\mathbb R$ alebo $X=\mathbb Z$ funkcia $f(x)=-x$ funguje ako kontrapríklad. Ale ak napríklad $X=\{0\}$, tak to kontrapríklad nie je.)
Skupina B: Viacerí z vás napísali niečo také, že ak na obe strany rovnosti $f\circ f=f$ aplikujeme $\inv f$, tak dostaneme $f=id_X$. To je pravda - ale len za predpokladu že $\inv f$ existuje; takže takýto argument prejde pre bijektívne zobrazenie $f$. (A hovorí nám to teda, že ak chceme nájsť kontrapríklad, musíme použiť nejakú funkciu, ktorá nie je bijektívna.)
Skupina D: Niektorí z vás poslali riešenie, kde nešlo o zobrazenia z tej istej množiny do tej istej množiny. Napríklad niečo podobné ako na obrázku, ktorý som ukázal vyššie:

Keďže mi chceme aby $f$ aj $g$ boli zobrazenia $X\to X$, tento kontrapríklad je trochu iný ako to čo sa chce v zadaní.
Takisto som dostal riešenie, kde bolo odvodené, že $g$ je surjektívne. A potom bolo tvrdenie, že z toho už vyplýva aj injektívnosť $g$.
Ako vidno z príkladu vyššie, toto nie je pravda.
Bola by to pravda pre konečnú množinu $X$ a zobrazenie $\Zobr gXX$. (A aj riešenie, kde bolo takéto tvrdenie uvedené, sa nejako odvolávalo na počet prvkov množiny $X$.)