Rôzne poznámky$\newcommand{\inv}[1]{{#1}^{-1}}\newcommand{\Zobr}[3]{#1\colon#2\to#3}$
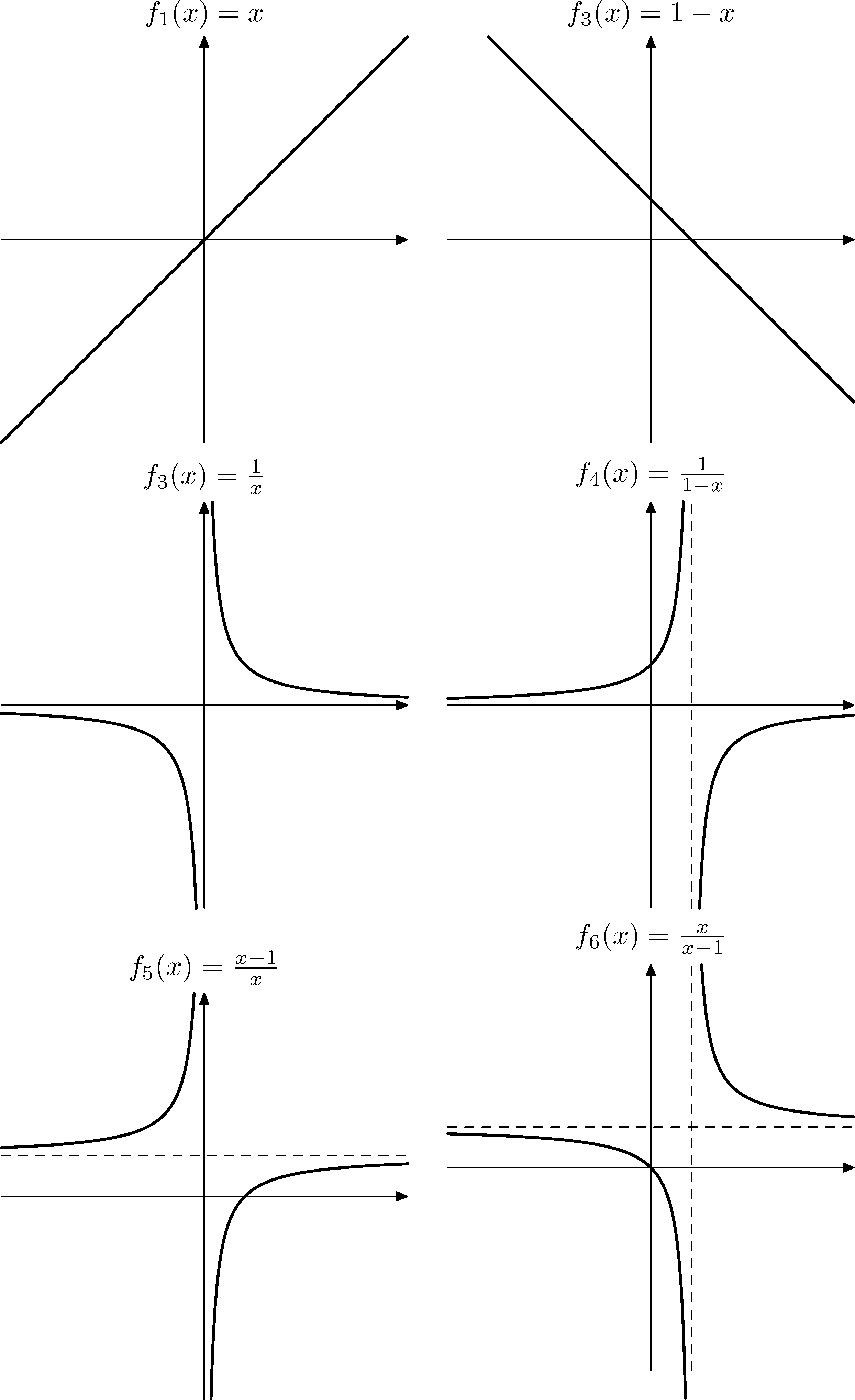
Uvažujme funkcie $\Zobr{f_i}{\mathbb R\setminus\{0,1\}}{\mathbb R\setminus\{0,1\}}$ definované ako
\begin{align*}
id(x)=f_1(x)&=x &f_4(x)&=\frac1{1-x}\\
f_2(x)&=\frac1x &f_5(x)&=\frac{x-1}x\\
f_3(x)&=1-x &f_6(x)&=\frac{x}{x-1}
\end{align*}
Označme $G=\{f_1,f_2,f_3,f_4,f_5,f_6\}$. Platí, že zloženie dvoch funkcií z $G$ opäť patrí do $G$. (Toto berte ako zadaný fakt, ktorý netreba overovať -- aj keď toto vlastne dostaneme, ak dáme dokopy veci, ktoré vypočítate pri riešení úloh v jednotlivých skupinách.)
Toto už nie je súčasťou zadania -- ale môžete sa zamyslieť aj nad tým, či sa nejako viete presvedčiť, že táto grupa je izomorfná s grupou $(S_3,\circ)$.
- Zistite, či každý prvok $f_i\in G$ je bijekcia a či $G$ obsahuje aj inverznú funkciu $\inv f_i$.
- Zdôvodnite, že $G$ s operáciou skladania zobrazení tvorí grupu.
- Vypočítajte, čomu sa rovnajú zložené zobrazenia uvedené pre vašu skupinu. (Uveďte aj postup, ktorým ste sa dostali k výsledku.)
A: $f_2\circ f_3$, $f_3\circ f_2$, $f_2\circ f_4$, $f_3\circ f_5$, $f_4\circ f_3$
B: $f_2\circ f_6$, $f_6\circ f_2$, $f_2\circ f_5$, $f_6\circ f_4$, $f_5\circ f_6$
C: $f_3\circ f_6$, $f_6\circ f_3$, $f_3\circ f_4$, $f_6\circ f_5$, $f_5\circ f_3$
D: $f_4\circ f_4$, $f_5\circ f_5$, $f_4\circ f_2$, $f_4\circ f_6$, $f_5\circ f_2$
Riešenie úlohy by sa v podstate nezmenilo, ak by sme mali rovnaké predpisy zobrazení a brali ich ako zobrazenia $\mathbb Q\setminus\{0,1\}\to\mathbb Q\setminus\{0,1\}$ resp. $\mathbb C\setminus\{0,1\}\to\mathbb C\setminus\{0,1\}$.
S touto grupou sa niekedy môžete stretnúť pod názvom anharmonic group: Wikipédia, Google, Google Books.
Môžeme si uvedomiť aj to, že sme opäť dostali nejaký príklad konečnej nekomutatívnej grupy. Aj keď na druhej strane sa dá povedať, že toto je príklad, ktorý sme už videli - keďže táto grupa je izomorfná s grupou $(S_3,\circ)$. Viac k izomorfizmu medzi týmito dvoma grupami: https://msleziak.com/forum/viewtopic.php?t=1729
Grafy funkcií
Môže byť aj užitočné nakresliť si grafy funkcií, s ktorými pracujeme. Môže to trochu pomôcť lepšie si uvedomiť, aké majú vlastnosti.
Všetky funkcie v tejto úlohe sú také, že sa so stredoškolskými vedomosťami dajú pomerne ľahko nakresliť. (Niekedy pomôže e3te si predpis funkcie trochu upraviť, aby sme ľahšie vedeli načrtnúť graf.)
Spoiler:
Tieto výrazy sú pre $x\ne0,1$ definované (nedostaneme nulu v menovateli.)
A tiež sa môžeme presvedčiť, že $f_i(x)\ne0$ a $f_i(x)\ne1$ buď priamo výpočtom alebo tak, že sa pozrieme na grafy.