Môžeme si všimnúť, že v prvom aj treťom grafe mám $v=8$ a $h=12$, čiže $h=2v-4$. Súčasne tam nie je žiadna kružnica dĺžky $3$.Ktoré z nasledujúcich grafov sú rovinné? Zdôvodnite!
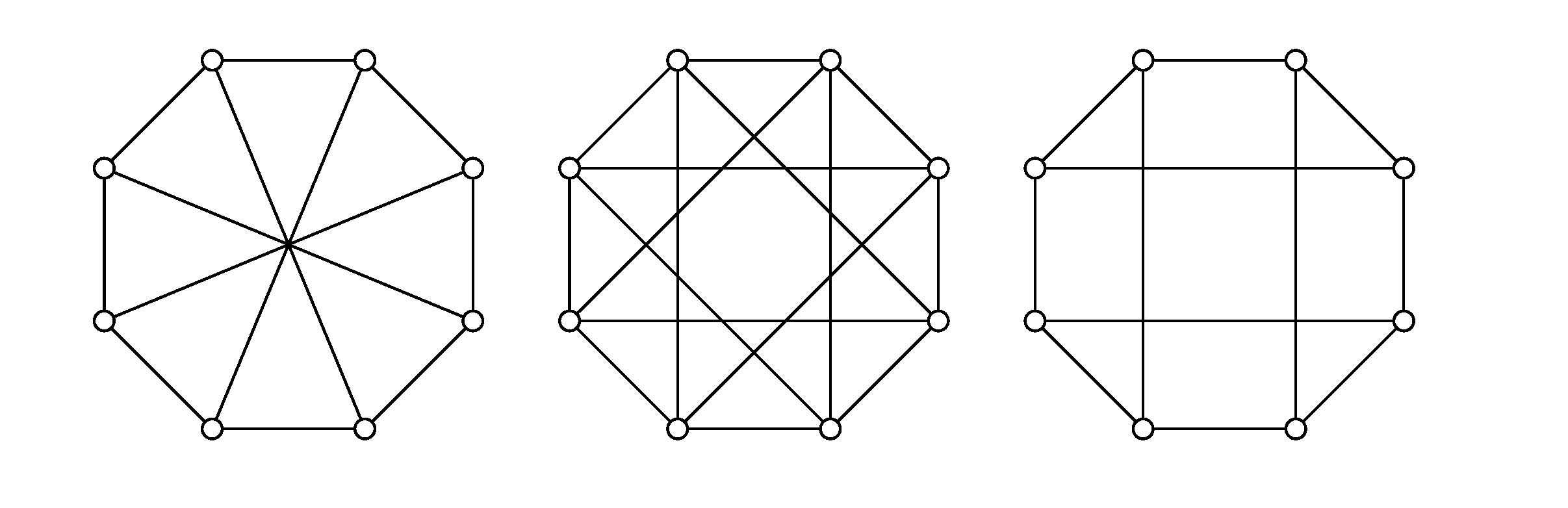
Keďže sa nadobúda rovnosť, pri akomkoľvek rovinnom nakreslení musí byť každá stena ohraničená kružnicou dĺžky $4.$
a) Nie je planárny. Graf $K_{3,3}$ viem dostať tak, že vynecháme jednu hranu a potom nahradíme vrcholy stupňa $2$ hranou.
Ak by mal pôvodný graf rovinné nakreslenie, tak by sme takýmito krokmi dostali rovinné nakreslenie pre $K_{3,3}$.
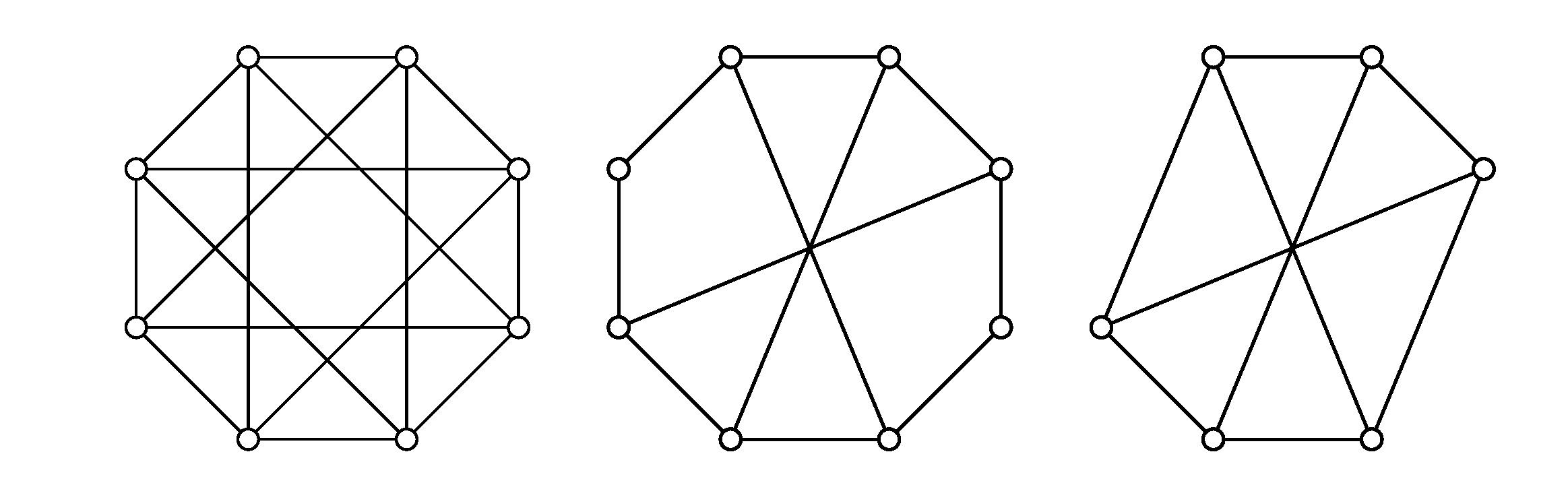
b) Nie je planárny. Je to $K_{4,4}$, teda obsahuje $K_{3,3}$ ako podgraf. (Pozri obrázok.)

Iná možnosť ako ukázať, že nie je rovinný je skontrolovať, že máme $h=16$, $v=8$ a neplatí nerovnosť $h\le 2v-4$. (A súčasne tam nemáme kružnice dĺžky $3$.)
c) Je planárny. Je to vlastne inak nakreslená kocka.