Ak $g\circ f$ je surjekcia, tak $f$ nemusí byť surjekcia
Posted: Fri Oct 12, 2018 1:45 pm
Zadanie
viewtopic.php?t=493
viewtopic.php?t=735
Ak si chcete pozrieť iné príklady z tejto témy (zobrazenia, skladenia, injekcie, surjekcie a pod.) čo sa vyskytli po minulé roky na písomke z výberového cvika, tak sa môžete pozrieť sem:
viewtopic.php?t=1153
Definícia. Zobrazenie $f\colon X\to Y$ je surjektívne ak $f[X]=Y$.
Inak povedané: Pre každý prvok $y\in Y$ existuje nejaké $x\in X$ také, že $f(x)=y$.
(Stručne: Každý prvok z $Y$ má aspoň jeden vzor.)
Riešenie
Chceme nájsť kontrapríklad, t.j. chceli by sme nájsť také zobrazenia, že $g\circ f$ nie je surjekcia, ale $f$ je surjekcia.
Azda skoro najjednoduchší príklad vyzerá takto:
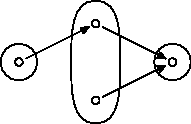
(Zobrali sme si skoro najjednoduchší možný príklad zobrazenie $f$ ktoré nie je surjektívne - t.j. potrebovali sme mať v strednej množine prvok na ktorý sa nič nezobrazí. A potom sme to skúsili nejako doplniť zobrazením $g$ tak, aby zloženie bolo surjektívne.)
Iný možný príklad (dá sa vymyslieť veľa ďalších):
$f\colon \mathbb R\to\mathbb R$, $g\colon \mathbb R \to [0,\infty)$, obe sú zadné predpisom
$f(x)=g(x)=|x|$.
Ak ich zložíme, tak máme zobrazenie $g\circ f\colon \mathbb R \to [0,\infty)$, ktoré je surjektívne. Ale zobrazenie $f$ nie je surjektívne.
(V oboch prípadoch sa na toto zobrazenie môžeme pozerať ako na absolútnu hodnotu. Ale ak sa na ňu pozeráme ako zobrazenie $\mathbb R \to [0,\infty)$ tak to je surjekcia, ale ak obor hodnôt je $\mathbb R$ tak to surjekcia nie je.)
Druhá skupina mala podobný príklad na injekcie. K nemu sa niečo dá nájsť tu:a) Napíšte definíciu surjektívneho zobrazenia.
b) Platí nasledujúce tvrdenie? Ak áno, dokážte ho, ak nie, nájdite kontrapríklad: Ak $f\colon X\to Y$ a $g\colon Y\to Z$ sú zobrazenia také, že $g\circ f$ je surjekcia, tak $f$ je surjekcia.
viewtopic.php?t=493
viewtopic.php?t=735
Ak si chcete pozrieť iné príklady z tejto témy (zobrazenia, skladenia, injekcie, surjekcie a pod.) čo sa vyskytli po minulé roky na písomke z výberového cvika, tak sa môžete pozrieť sem:
viewtopic.php?t=1153
Definícia. Zobrazenie $f\colon X\to Y$ je surjektívne ak $f[X]=Y$.
Inak povedané: Pre každý prvok $y\in Y$ existuje nejaké $x\in X$ také, že $f(x)=y$.
(Stručne: Každý prvok z $Y$ má aspoň jeden vzor.)
Riešenie
Chceme nájsť kontrapríklad, t.j. chceli by sme nájsť také zobrazenia, že $g\circ f$ nie je surjekcia, ale $f$ je surjekcia.
Azda skoro najjednoduchší príklad vyzerá takto:

(Zobrali sme si skoro najjednoduchší možný príklad zobrazenie $f$ ktoré nie je surjektívne - t.j. potrebovali sme mať v strednej množine prvok na ktorý sa nič nezobrazí. A potom sme to skúsili nejako doplniť zobrazením $g$ tak, aby zloženie bolo surjektívne.)
Iný možný príklad (dá sa vymyslieť veľa ďalších):
$f\colon \mathbb R\to\mathbb R$, $g\colon \mathbb R \to [0,\infty)$, obe sú zadné predpisom
$f(x)=g(x)=|x|$.
Ak ich zložíme, tak máme zobrazenie $g\circ f\colon \mathbb R \to [0,\infty)$, ktoré je surjektívne. Ale zobrazenie $f$ nie je surjektívne.
(V oboch prípadoch sa na toto zobrazenie môžeme pozerať ako na absolútnu hodnotu. Ale ak sa na ňu pozeráme ako zobrazenie $\mathbb R \to [0,\infty)$ tak to je surjekcia, ale ak obor hodnôt je $\mathbb R$ tak to surjekcia nie je.)