msleziak.com

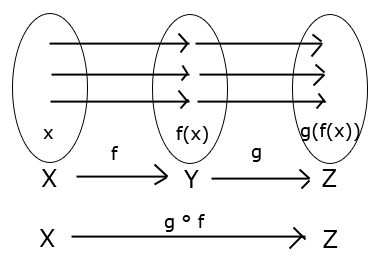
Úloha 1.1. Dokážte: Ak $g\circ f$ je injekcia, tak $f$ je injekcia. Platí aj opačná implikácia? Musí $g$ byť injekcia?

---

Vychádzam z predpokladu, že $g\circ f$ je injekcia. Potom by malo platiť:

$g\circ f(x) = g\circ f(y)$

$g(f(x)) = g(f(y))$

$f(x) = f(y)$

Keďže zobrazenie $g\circ f$ je injekcia, musí platiť aj $x = y$ (malo by to vychádzať z definície) a preto si myslím, že funkcia $f$ je injektívna.

---

Platí táto implikácia aj opačne? Teda: platí, že ak $f$ je injekcia, tak aj $g\circ f$ je injekcia ?

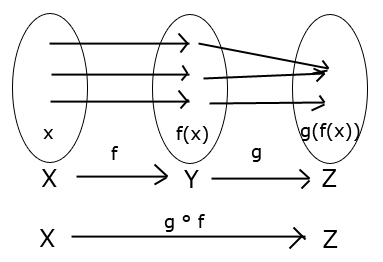
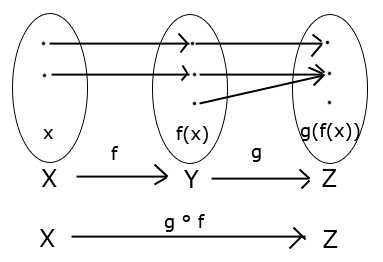
Myslím, že neplatí, lebo v prípade, že by funkcia $g$ nebola injektívna, nemohlo by zobrazenie $g\circ f$ byť injektívne.

Inými slovami, aby sme dostali injektívne zložené zobrazenie, obe funkcie, vrátane funkcie $g$ musia byť injektívne. Ak to tak nie je, rád sa nechám vyviesť z omylu

ErikVarga108 wrote: Vychádzam z predpokladu, že $g\circ f$ je injekcia. Potom by malo platiť:

$g\circ f(x) = g\circ f(y)$

$g(f(x)) = g(f(y))$

$f(x) = f(y)$

Keďže zobrazenie $g\circ f$ je injekcia, musí platiť aj $x = y$ (malo by to vychádzať z definície) a preto si myslím, že funkcia $f$ je injektívna.

Dohodnime sa, že táto prvá časť je ok (=ok z toho hľadiska, či za ňu dostanete body), aj keď pokec vysvetľujúci váš postup nie je celkom správny.
Správnejšie by bolo povedať, že: keď chceme dokázať, že $g\circ f$ je injekcia, tak vlastne chceme overiť implikáciu $g\circ f(x)=g\circ f(y)$ $\Rightarrow$ $x=y$.
Takže začneme tým, že budeme predpokladať, že pre nejaké $x$, $y$ platí $g\circ f(x)=g\circ f(y)$ a budeme sa snažiť odvodiť $x=y$.
Po tomto úvode už všetky ďalšie kroky, ktoré ste napísali, sedia s tým, čo chceme robiť.

OPRAVA: Mal som napísať toto. Dokazujeme, že $f$ je injekcia. (Omylom som napísal $g\circ f$.)
Teda vychádzame z predpokladu $f(x)=f(y)$.
Z neho dostaneme, že aj $g(f(x))=g(f(y))$.
Na tomto mieste využijeme, že $g\circ f$ je injekcia a dostaneme $x=y$-
Skontrolovali sme, že z $f(x)=f(y)$ vyplýva $x=y$.

ErikVarga108 wrote: Platí táto implikácia aj opačne? Teda: platí, že ak $f$ je injekcia, tak aj $g\circ f$ je injekcia ?

Myslím, že neplatí, lebo v prípade, že by funkcia $g$ nebola injektívna, nemohlo by zobrazenie $g\circ f$ byť injektívne.

Inými slovami, aby sme dostali injektívne zložené zobrazenie, obe funkcie, vrátane funkcie $g$ musia byť injektívne. Ak to tak nie je, rád sa nechám vyviesť z omylu

Ak si myslíte, že to platí, mali by ste to aj dokázať.
V skutočnosti neplatí, to čo ste tvrdili, t.j. nie je pravda, že: $g\circ f$ je injektívne $\Rightarrow$ $g$ je injektívne.
Aby som vás presvedčil, že to je tak, mal by som nájsť konkrétny príklad funkcií takých, že zloženie $g\circ f$ je injektívne, ale funkcia $g$ nie je injektívna.
Nebudem sem však (aspoň zatiaľ) taký príklad písať, lebo toto je vlastne súčasť úlohy. Mali ste si rozmyslieť, či táto vec platí (vy ste napísali, že áno; ja už som vám prezradil, že nie). Ešte treba nejako zdôvodniť, že neplatí - t.j. nájsť konkrétny príklad, na ktorom to ukážete. (Resp. ak ste presvedčený, že to platí - a minimálne keď ste posielali predošlý post, tak ste si zjavne mysleli, že to platí - tak by tu mal byť dôkaz, že to je naozaj tak. Skúsiť tvrdenie dokazovať možno tiež nemusí byť zlá taktika, aj ak ešte nevieme či platí. Môže sa stať, že pri dôkaze narazíme na problémy a keď budeme vidieť v čom presne bol problém pri dôkaze, ta nám to môže pomôcť nájsť kontrapríklad.)

Pre istotu (ak to nebolo z môjho predchádzajúceho príspevku jasné), tak sem ešte explicitne napíšem, že od vás očakávam, že sa pokúsite nájsť kontrapríklad na druhú časť úlohy. Ak sa vám to podarí, tak by táto úloha mohla byť za plný počet bodov (t.j. 1 bod, ale plný počet znie lepšie).

Dobre. Nedarí sa mi taký kontrapríklad nájsť, preto zdôvodním, ako som sa dopracoval k tej úvahe, že aj $g$ musí byť injektívna (k tej, ktorá už teda neplatí, ale možno mi na základe toho dáte ešte nejaký tip, čo robím zle).

$f: X \rightarrow Y$
$g: Y \rightarrow Z$
$g\circ f: X \rightarrow Z$

$f$ je injektívna. To znamená, že každé $x$ zobrazí na inú funkčnú hodnotu $f(x)$. V mojom riešení som považoval aj $g$ za nutne injektívnu, aby mohlo nastať takéto niečo:

Každé $f(x)$ sa opäť zobrazí na iné $g(f(x))$ a nestane sa, že sa dva prvky zobrazia na ten istý (tak chápem injekciu).

Ak hľadám protipríklad, čiže $g$ nemá byť injektívna, vždy som schopný sa dopracovať len k niečomu v tomto štýle:

Prípadne zobrazím všetky $f(x)$ na rovnaké $g(f(x))$.

Každopádne to znamená, že $g\circ f$ nie je ako celok injektívna, lebo nie úplne všetky prvky z množiny $X$ sa zobrazia na rôzne hodnoty v množine $Z$. To znamená že zobrazenie nie je injektívne.

Možno niečo prehliadam, alebo mám používať jednoprvkové množiny. V takom prípade si ale skutočne zatiaľ nie som istý, čo s tým ďalej.

Ešte snáď doplňujúca otázka aj pre budúcnosť (a ostatných): je možné dostať napr. 0,5 boda, alebo len celé?

Skúste trochu zmodifikovať ten váš posledný obrázok - zamyslite sa, čo by sa stalo, keby ste prvú množinu zvolili dvojprvkovú. (T.j. napríklad X má 2 prvky, Y aj Z majú 3 prvky.) Alebo X jednoprvkovú a ostatné nechať.

ErikVarga108 wrote:Ešte snáď doplňujúca otázka aj pre budúcnosť (a ostatných): je možné dostať napr. 0,5 boda, alebo len celé?

Áno dá sa dostať 0.5 bodu. (Aj keď snáď s týmto hintom sa vám už podarí nájsť kontrapríklad a bude to za 1 bod.)

Ak predošlý hint nepomohol a túto úlohu už vzdávate, tak to sem napíšte - aby vaši spolužiaci vedeli, že druhá časť úlohy je "voľná" a získať toho zvyšného pol bodu môže skúsiť niekto iný.

Ďakujem, asi chápem, neuvedomil som si, že pri injekcii nemusí byť obsadená celá množina, na ktorú sa zobrazuje $x$.

Teraz je myslím celé zložené zobrazenie injektívne, hoci $g$ nie je.

Konkrétny príklad mi napadol len taký jednoduchý (nie som si istý, či to stačí):
$X:$ {$0, 1$}
$Y:$ {$1, 2, 3$}
$Z:$ {$1, 2, 3$}

$f: X \rightarrow Y$
$g: Y \rightarrow Z$
$g\circ f: X \rightarrow Z$

$f(x) = x+1$ (0 sa zobrazí na 1, 1 na 2)
$g(f(x)):$
- ak $f(x) \leq 1: g(f(x)) = 1$ (1 sa zobrazí na 1)
- ak $f(x) > 1: g(f(x)) = 2$ (2, 3 sa obe zobrazia na 2 - preto $g$ nie je injektívna)

Výsledné zobrazenie $g\circ f$ bude injektívne, lebo každý prvok z množiny $X$ sa zobrazí na iný prvok množiny $Z$. To, že nie sú obsadené všetky prvky zo $Z$, nevadí.

Tento príklad je v poriadku.

Ešte jednoduchší príklad by sme dostali, keby sme zobrali za X jednoprvkovú množinu. (Je ľahké uvedomiť si, že každé zobrazenie idúce z jednoprvkovej množiny je injektívne, čiže $g\circ f$ bude injektívne bez ohľadu na to, ako si zvolíme $g$.)

Značím si za túto úlohu 1 bod.