Ak $g\circ f$ je injekcia, musí byť aj $g$ injekcia?
Posted: Wed Oct 08, 2014 3:39 pm
Príklad z písomky na výberovom cviku bol:
Teda chceme nájsť príklad zobrazení takých, že $g$ je injekcia, ale $g\circ f$ nie je injekcia. (Implikácia je nepravdivá iba v prípade $1\Rightarrow0$, t.j. ak predpoklady implikácie sú splnené, ale neplatí tvrdenie na pravej strane implikácie.)
Chceme teda, aby $g$ nebolo injektívne, čiže potrebujeme, aby $g$ zobrazovalo dva rôzne prvky na ten istý prvok. Najjednoduchšie také zobrazenie dostaneme tak, že zobrazíme dvojprvkovú množinu na jednoprvkovú.
Teraz chceme vymyslieť $f$ tak, aby zloženie $g\circ f$ bolo injektívne. Opäť, keď skúsime čo najjednoduchší možný prípad, tak to vyjde.
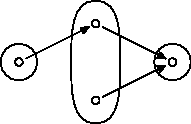
Teda náš kontrapríklad môžeme zapísať takto:
$X=\{0\}$, $Y=\{0,1\}$, $Z=\{0\}$;
$f\colon X\to Y$ je definované ako $f(0)=0$;
$g\colon Y\to Z$ je definované ako $g(0)=g(1)=0$.
Odpoveď je, že tvrdenie neplatí. Kontrapríklad nie je príliš ťažké nájsť. Uvedomme si najprv čo vlastne hľadáme. Pýtame sa, či vieme nájsť kontrapríklad k implikácii: $g\circ f$ je injekcia $\Rightarrow$ $g$ je injekcia.a) Napíšte definíciu injektívneho zobrazenia.
b) Platí nasledujúce tvrdenie? Ak áno, dokážte ho, ak nie, nájdite kontrapríklad: Ak $f\colon X\to Y$ a $g\colon Y\to Z$ sú zobrazenia také, že $g\circ f$ je injekcia, tak $g$ je injekcia.
Teda chceme nájsť príklad zobrazení takých, že $g$ je injekcia, ale $g\circ f$ nie je injekcia. (Implikácia je nepravdivá iba v prípade $1\Rightarrow0$, t.j. ak predpoklady implikácie sú splnené, ale neplatí tvrdenie na pravej strane implikácie.)
Chceme teda, aby $g$ nebolo injektívne, čiže potrebujeme, aby $g$ zobrazovalo dva rôzne prvky na ten istý prvok. Najjednoduchšie také zobrazenie dostaneme tak, že zobrazíme dvojprvkovú množinu na jednoprvkovú.
Teraz chceme vymyslieť $f$ tak, aby zloženie $g\circ f$ bolo injektívne. Opäť, keď skúsime čo najjednoduchší možný prípad, tak to vyjde.

Teda náš kontrapríklad môžeme zapísať takto:
$X=\{0\}$, $Y=\{0,1\}$, $Z=\{0\}$;
$f\colon X\to Y$ je definované ako $f(0)=0$;
$g\colon Y\to Z$ je definované ako $g(0)=g(1)=0$.