Nový predmet - Aplikácie teórie množín
Posted: Fri Jan 23, 2015 10:42 am
Tento semester by sa mal prvýkrát otvárať predmet Aplikácie teórie množín (2-MAT-226).
Nejaké základné informácie si môžete prečítať v informačnom liste. Tu by som chcel doplniť nejaké ďalšie informácie.
Tento predmet by sa mal - ak všetko pôjde podľa plánu - otvárať raz za dva roky. V rokoch, keď bude suspendovaný, pobeží predmet Seminár z teórie čísel. (Túto informáciu viete aj z ročenky resp. zo študijného plánu). Tento predmet je v študijnom pláne pre študentov magisterského štúdia odboru matematika. (Ale netvrdím, že je nezvládnuteľný povedzme pre tretiaka na bakalárskom štúdiu. Určite však každý, kto si naň trúfne, by mal dobre ovládať prinajmenšom veci z prváckej diskrétnej matematiky.)
Text k prednáške
Na stránke predmetu nájdete nedokončenú verziu textu s nejakými poznámkami k prednáške. Do začiatku semestra by som tam ešte rád stihol nejaké veci doplniť (a takisto budem ten text priebežnu upravovať aj počas semestra) ale aspoň nejakú základnú predstavu o tom, čo by sme mali preberať, by sa malo z neho dať získať.
Prvá kapitola obsahuje len nejaký úvodný pokec. (Ale môže sa oplatiť si niečo z nej prečítať, aby ste vedeli, o čom zhruba bude reč. Najmä ak sa rozhodujete, či si tento predmet zapíšete.) V druhej kapitole sú len zopakované nejaké veci, ktoré by ste mali už ovládať. Tretia kapitola je venovaná najmä axiomatickej teórie množín. Pre účely tejto prednášky však nie je až také dôležité ho detailne ovládať, dôležité je porozumieť tomu, aký je rozdiel medzi naivnou a axiomatickou teóriou množín a pre aké účely môže byť axiomatický pohľad užitočný. Samotné jadro prednášky teda začína až v štvrtej kapitole.
Uvidíme, ako rýchlo sa nám bude na prednáške dariť napredovať. (Tým, že je táto prednáška otvorená prvýkrát, nemám úplne dobrý odhad, čo všetko stihnem. Takisto sa snáď podarí text k prednáške časom dostať do nejakej ucelenejšej podoby, než v akej je teraz a vychytať nejaké chyby, ktoré sa tam určite dostali.) Určite však chcem stihnúť prebrať minimálne veci o Zornovej leme a o transfinitnej indukcii. Ak sa podarí, tak aj nejaké ďalšie veci.
V texte sú aj rôzne veci, ktoré neplánujem preberať (alebo ich s veľkou pravdepodobnosťou nestihnem). Niektoré sú aj vyznačené ako nepovinné. Sú to veci, ktoré súvisia so zaradenou látkou a z rôznych dôvodov sa mi zdalo vhodné niečo napísať aj o nich.
Obsah prednášky
Asi lepšiu predstavu o témach, ktoré by som chcel preberať, získate zo spomínaného textu. Ale aspoň stručne by som chcel niečo povedať aj tu.
Dá sa povedať, že dve najdôležitejšie témy, ktorými sa chceme zaoberať, sú axióma výberu (najmä v podobe Zornovej lemy) a transfinitná indukcia. Obidve sú vcelku užitočné dôkazové techniky. (Je veľmi pravdepodobné, že aspoň s jednou z nich ste sa už na niektorom predmete stretli. A celkom určite ste používali mnohé dôsledky axiómy výberu. Keď si pozriete napríklad na Wikipédii zoznam niektorých tvrdení, ktoré vyplývajú z axiómy výberu alebo sú s ňou dokonca ekvivalentné, tak veľa z nich by ste mali poznať a vedieť, že sú dôležité.) Tu by sme sa chceli trochu pozrieť na to, prečo tieto techniky fungujú, čiže dokázať ich správnosť - na to možno inde, kde ste ich používali, nemusel zvýšiť čas. A tiež by sme si chceli ukázať ich aplikácie axiómy výberu a transfinitnej indukcie; možno trochu detailnejšie, než ste ich videli inde.
Je vcelku možné, že veľa z týchto vecí už viete. Ale aj ak je to tak, nemusí byť nutne na škodu si ich zopakovať. (A dúfam, že sa na tejto prednáške dozviete aj niečo nové.) Aj ak by sme toho nestihli viac, iba tieto dve témy, tak by som považoval túto prednášku za užitočnú. Ale ak sa podarí, rád by som ukázal aj aplikácie nejakých ďalších pekných vecí, ako napríklad ultrafiltrov (a ultralimít), nekonečných stromov či skoro disjunktných systémov.
Hodnotenie
Neviem, do akej miery vaše rozhodovanie, či si predmet zapísať, ovplyvňuje aj to, ako bude predmet hodnotený. Ešte nemám úplne detailne rozmyslené hodnotenie. (Mám ešte pár týždňov na to aby som sa rozhodol.) Ale môžem napísať aspoň, čo mám rozmyslené.
Ochutnávka
Nech to funguje trochu aj ako reklama, tak skúsim pridať aspoň niečo, čo tam chcem preberať a mohlo by to vyzerať aspoň trochu zaujímavé.
Napríklad pomocou transfinitnej indukcie dokážeme, že existuje funkcia $f\colon{\mathbb R}\to{\mathbb R}$, ktorá na každom intervale nadobúda všetky reálne hodnoty. (Snáď aspoň trochu vidno, že takáto funkcia vyzerá byť pomerne neobvykle, skoro by sa dalo povedať, že až patologicky.) Transfinitná indukcia nie je jediná možnosť ako dostať takúto funkciu, dokonca by sme vedeli nájsť aj explicitný predpis pre takú funkciu. Rôzne dôkazy existencie takejto funkcie môžete nájsť napríklad tu, tu alebo tu. Každopádne transfinitnou indukciou budeme vedieť dostať aj iné objekty, na prvý pohľad vyzerajúce kontraintuitívne.
Aby ste sa pri čítaní textu nenudili, sú tam aj nejaké pekné obrázky, ako napríklad tento:
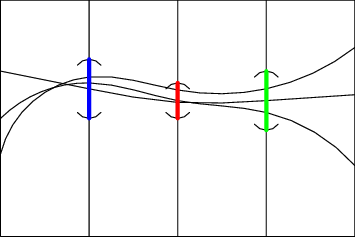
Obrázok ilustruje ako vyzerá subbáza súčinovej topológie. Na prednáške by som chcel ukázať pomerne jednoduchý dôkaz Tichonovovej vety založený na Alexandrovej vete o subbáze. Práve dôkaz Alexandrovej vety o subbáze urobíme pomocou Zornovej lemy.
Nejaké základné informácie si môžete prečítať v informačnom liste. Tu by som chcel doplniť nejaké ďalšie informácie.
Tento predmet by sa mal - ak všetko pôjde podľa plánu - otvárať raz za dva roky. V rokoch, keď bude suspendovaný, pobeží predmet Seminár z teórie čísel. (Túto informáciu viete aj z ročenky resp. zo študijného plánu). Tento predmet je v študijnom pláne pre študentov magisterského štúdia odboru matematika. (Ale netvrdím, že je nezvládnuteľný povedzme pre tretiaka na bakalárskom štúdiu. Určite však každý, kto si naň trúfne, by mal dobre ovládať prinajmenšom veci z prváckej diskrétnej matematiky.)
Text k prednáške
Na stránke predmetu nájdete nedokončenú verziu textu s nejakými poznámkami k prednáške. Do začiatku semestra by som tam ešte rád stihol nejaké veci doplniť (a takisto budem ten text priebežnu upravovať aj počas semestra) ale aspoň nejakú základnú predstavu o tom, čo by sme mali preberať, by sa malo z neho dať získať.
Prvá kapitola obsahuje len nejaký úvodný pokec. (Ale môže sa oplatiť si niečo z nej prečítať, aby ste vedeli, o čom zhruba bude reč. Najmä ak sa rozhodujete, či si tento predmet zapíšete.) V druhej kapitole sú len zopakované nejaké veci, ktoré by ste mali už ovládať. Tretia kapitola je venovaná najmä axiomatickej teórie množín. Pre účely tejto prednášky však nie je až také dôležité ho detailne ovládať, dôležité je porozumieť tomu, aký je rozdiel medzi naivnou a axiomatickou teóriou množín a pre aké účely môže byť axiomatický pohľad užitočný. Samotné jadro prednášky teda začína až v štvrtej kapitole.
Uvidíme, ako rýchlo sa nám bude na prednáške dariť napredovať. (Tým, že je táto prednáška otvorená prvýkrát, nemám úplne dobrý odhad, čo všetko stihnem. Takisto sa snáď podarí text k prednáške časom dostať do nejakej ucelenejšej podoby, než v akej je teraz a vychytať nejaké chyby, ktoré sa tam určite dostali.) Určite však chcem stihnúť prebrať minimálne veci o Zornovej leme a o transfinitnej indukcii. Ak sa podarí, tak aj nejaké ďalšie veci.
V texte sú aj rôzne veci, ktoré neplánujem preberať (alebo ich s veľkou pravdepodobnosťou nestihnem). Niektoré sú aj vyznačené ako nepovinné. Sú to veci, ktoré súvisia so zaradenou látkou a z rôznych dôvodov sa mi zdalo vhodné niečo napísať aj o nich.
Obsah prednášky
Asi lepšiu predstavu o témach, ktoré by som chcel preberať, získate zo spomínaného textu. Ale aspoň stručne by som chcel niečo povedať aj tu.
Dá sa povedať, že dve najdôležitejšie témy, ktorými sa chceme zaoberať, sú axióma výberu (najmä v podobe Zornovej lemy) a transfinitná indukcia. Obidve sú vcelku užitočné dôkazové techniky. (Je veľmi pravdepodobné, že aspoň s jednou z nich ste sa už na niektorom predmete stretli. A celkom určite ste používali mnohé dôsledky axiómy výberu. Keď si pozriete napríklad na Wikipédii zoznam niektorých tvrdení, ktoré vyplývajú z axiómy výberu alebo sú s ňou dokonca ekvivalentné, tak veľa z nich by ste mali poznať a vedieť, že sú dôležité.) Tu by sme sa chceli trochu pozrieť na to, prečo tieto techniky fungujú, čiže dokázať ich správnosť - na to možno inde, kde ste ich používali, nemusel zvýšiť čas. A tiež by sme si chceli ukázať ich aplikácie axiómy výberu a transfinitnej indukcie; možno trochu detailnejšie, než ste ich videli inde.
Je vcelku možné, že veľa z týchto vecí už viete. Ale aj ak je to tak, nemusí byť nutne na škodu si ich zopakovať. (A dúfam, že sa na tejto prednáške dozviete aj niečo nové.) Aj ak by sme toho nestihli viac, iba tieto dve témy, tak by som považoval túto prednášku za užitočnú. Ale ak sa podarí, rád by som ukázal aj aplikácie nejakých ďalších pekných vecí, ako napríklad ultrafiltrov (a ultralimít), nekonečných stromov či skoro disjunktných systémov.
Hodnotenie
Neviem, do akej miery vaše rozhodovanie, či si predmet zapísať, ovplyvňuje aj to, ako bude predmet hodnotený. Ešte nemám úplne detailne rozmyslené hodnotenie. (Mám ešte pár týždňov na to aby som sa rozhodol.) Ale môžem napísať aspoň, čo mám rozmyslené.
- Určite budú nejaké domáce úlohy. (Zhruba takej náročnosti, ako sú cvičenia uvedené v texte.)
- Okrem toho v texte sú uvedené viaceré problémy - takto som nazval dlhšie cvičenia, ktoré sú náročnejšie a zvyčajne majú viacero častí. Zosumarizované sú v časti 1.3. (Do začiatku semestra tam chcem stihnúť ešte zopár ďalších problémov pridať.) Budem od vás chcieť, aby každý odovzdal riešenie 3 problémov; jedného na Zornovu lemu, jedného na transfinitnú indukciu a ešte jedného z ostatných oblastí. Ak by zvýšil čas, tak niektoré z nich by ste mohli aj odprezentovať na hodine. (Detailnejšie by sme sa dohodli na začiatku semestra, začiatkom semestra by ste sa mali aj možnosť sa prihlásiť, kto si vyberie ktorý problém.) Táto časť by tvorila minimálne 50% známky.
- Nemám v pláne robiť skúšku. Ešte zvážim, či ku koncu semestra nedám ešte nejaký take-home-test, s pár otázkami, ktoré by ste vypracovali a odovzdali.
Ochutnávka
Nech to funguje trochu aj ako reklama, tak skúsim pridať aspoň niečo, čo tam chcem preberať a mohlo by to vyzerať aspoň trochu zaujímavé.
Napríklad pomocou transfinitnej indukcie dokážeme, že existuje funkcia $f\colon{\mathbb R}\to{\mathbb R}$, ktorá na každom intervale nadobúda všetky reálne hodnoty. (Snáď aspoň trochu vidno, že takáto funkcia vyzerá byť pomerne neobvykle, skoro by sa dalo povedať, že až patologicky.) Transfinitná indukcia nie je jediná možnosť ako dostať takúto funkciu, dokonca by sme vedeli nájsť aj explicitný predpis pre takú funkciu. Rôzne dôkazy existencie takejto funkcie môžete nájsť napríklad tu, tu alebo tu. Každopádne transfinitnou indukciou budeme vedieť dostať aj iné objekty, na prvý pohľad vyzerajúce kontraintuitívne.
Aby ste sa pri čítaní textu nenudili, sú tam aj nejaké pekné obrázky, ako napríklad tento:

Obrázok ilustruje ako vyzerá subbáza súčinovej topológie. Na prednáške by som chcel ukázať pomerne jednoduchý dôkaz Tichonovovej vety založený na Alexandrovej vete o subbáze. Práve dôkaz Alexandrovej vety o subbáze urobíme pomocou Zornovej lemy.