Injekcie a skladanie
Posted: Sun Oct 11, 2015 5:15 pm
Úloha z písomky:
Zobrazenie $f\colon X\to Y$ je injektívne, ak platí
$$(\forall x_{1,2}\in X) f(x_1)=f(x_2) \Rightarrow x_1=x_2.$$
Túto definíciu môžeme ekvivalentne zapísať (obmena implikácie):
$$(\forall x_{1,2}\in X) x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2).$$
V niektorých písomkách ste tvrdili, že definícia injekcie je
$$(\forall x_{1,2}\in X) f(x_1) \ne f(x_2) \Rightarrow x_1 \ne x_2.$$
Toto nie je správna definícia. Môžeme si však rozmyslieť, čo táto vlastnosť hovorí. Možno sa oplatí pozrieť na obmenenú implikáciu:
$$(\forall x_{1,2}\in X) x_1=x_2 \Rightarrow f(x_1)=f(x_2).$$
Keď ju máme zapísanú takto, tak vidíme, že táto vlastnosť platí pre každé zobrazenie. Hovorí to presne to, že ku každému prvku z $X$ máme práve jeden obraz. (Jeden prvok sa nemôže zobraziť na dve rozličné veci.)
Kontrapríklad
V druhej časti som sa pýtal na platnosť tvrdenia:
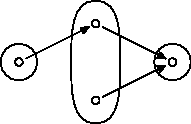
Vidíme, že $g\circ f$ je injekcia. Ale zobrazenie $g$ nie je injektívne.
Niekto navrhol takýto kontrapríklad:
$g \colon \mathbb R \to \mathbb R^+$; $g(x)=x^2$
$f \colon \mathbb R^+ \to \mathbb R$; $f(x)=\sqrt{x}$
Symbol $\mathbb R^+$ označuje množinu reálnych čísel.
Toto je tiež správny kontrapríklad.
Ak sa pozrieme na zložené zobrazenie, tak $g\circ f(x)=\sqrt{x^2}=x$, čiže je to identické zobrazenie na množine $\mathbb R^+$, ktoré je skutočne injektívne.
(Pre istotu upozorním, že rovnosť $\sqrt{x^2}=x$ sme mohli napísať vďaka tomu, že $x\ge0$. Vo všeobecnosti pre reálne čísla vieme iba $\sqrt{x^2}=|x|$.)
Zobrazenie $g$ však nie je injektívne, lebo napríklad $g(1)=g(-1)=1$.
Definícia injektívneho zobrazeniaa) Napíšte definíciu injektívneho zobrazenia.
b) Platí nasledujúce tvrdenie? Ak áno, dokážte ho, ak nie, nájdite kontrapríklad: Ak $f\colon X\to Y$ a $g\colon Y\to Z$ sú zobrazenia také, že $g\circ f$ je injekcia, tak $g$ je injekcia.
Zobrazenie $f\colon X\to Y$ je injektívne, ak platí
$$(\forall x_{1,2}\in X) f(x_1)=f(x_2) \Rightarrow x_1=x_2.$$
Túto definíciu môžeme ekvivalentne zapísať (obmena implikácie):
$$(\forall x_{1,2}\in X) x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2).$$
V niektorých písomkách ste tvrdili, že definícia injekcie je
$$(\forall x_{1,2}\in X) f(x_1) \ne f(x_2) \Rightarrow x_1 \ne x_2.$$
Toto nie je správna definícia. Môžeme si však rozmyslieť, čo táto vlastnosť hovorí. Možno sa oplatí pozrieť na obmenenú implikáciu:
$$(\forall x_{1,2}\in X) x_1=x_2 \Rightarrow f(x_1)=f(x_2).$$
Keď ju máme zapísanú takto, tak vidíme, že táto vlastnosť platí pre každé zobrazenie. Hovorí to presne to, že ku každému prvku z $X$ máme práve jeden obraz. (Jeden prvok sa nemôže zobraziť na dve rozličné veci.)
Kontrapríklad
V druhej časti som sa pýtal na platnosť tvrdenia:
Toto tvrdenie neplatí. Azda najjednoduchší kontrapríklad vyzerá takto:Ak $f\colon X\to Y$ a $g\colon Y\to Z$ sú zobrazenia také, že $g\circ f$ je injekcia, tak $g$ je injekcia.

Vidíme, že $g\circ f$ je injekcia. Ale zobrazenie $g$ nie je injektívne.
Niekto navrhol takýto kontrapríklad:
$g \colon \mathbb R \to \mathbb R^+$; $g(x)=x^2$
$f \colon \mathbb R^+ \to \mathbb R$; $f(x)=\sqrt{x}$
Symbol $\mathbb R^+$ označuje množinu reálnych čísel.
Toto je tiež správny kontrapríklad.
Ak sa pozrieme na zložené zobrazenie, tak $g\circ f(x)=\sqrt{x^2}=x$, čiže je to identické zobrazenie na množine $\mathbb R^+$, ktoré je skutočne injektívne.
(Pre istotu upozorním, že rovnosť $\sqrt{x^2}=x$ sme mohli napísať vďaka tomu, že $x\ge0$. Vo všeobecnosti pre reálne čísla vieme iba $\sqrt{x^2}=|x|$.)
Zobrazenie $g$ však nie je injektívne, lebo napríklad $g(1)=g(-1)=1$.