msleziak.com

Napíšem sem zadania a stručne niečo k riešeniam.
Ak by k niektorej úlohe bolo treba detailnejší komentár, máte k nej ďalšie otázky, alebo treba niečo dovysvetliť, tak je asi najlepšie otvoriť nový topic. (Samozrejme, skopírujte odtiaľto, čo treba.)

Skupina A

1. Platí nasledujúce tvrdenie? Ak áno, dokážte ho, ak nie, nájdite kontrapríklad: Ak $f\colon X\to Y$ a $g\colon Y\to Z$ sú zobrazenia také, že $g\circ f$ je injekcia, tak $g$ je injekcia.

2. Na $\mathbb R\times\mathbb R$ definujeme operácie $+$ a $\cdot$ takto: $(a,b)+(c,d)=(a+c,b+d)$ a $(a,b).(c,d)=(ac,bd)$. Je $\mathbb R\times\mathbb R$ s týmito operáciami pole?

3. Vieme, že $\mathbb R$ je vektorový priestor nad $\mathbb Q$ (s obvyklým sčitovaním a násobením). Ukážte, že v tomto vektorovom priestore sú vektory $1$, $\sqrt2$, $\sqrt3$ lineárne nezávislé.

4. a) Sú vektory $(1,2,3)$, $(1,3,3)$ a $(3,0,4)$ lineárne nezávislé nad $\mathbb Z_5$?
b) Sú vektory $(1,3,3)$, $(2,1,4)$, $(2,1,2)$ a $(1,3,4)$ lineárne nezávislé nad $\mathbb Z_5$?
c) Doplňte vektory $(1,0,1)$, $(2,1,3)$ na bázu priestoru $(\mathbb Z_5)^3$.

5*. Ak pre každý prvok $x$ grupy $(G,\circ)$ platí $x\circ x=e$, tak táto grupa je komutatívna.

Skupina B

1. Platí nasledujúce tvrdenie? Ak áno, dokážte ho, ak nie, nájdite kontrapríklad: Ak $f\colon X\to Y$ a $g\colon Y\to Z$ sú zobrazenia také, že $g\circ f$ je surjekcia, tak $f$ je surjekcia.

2. Je $\mathbb R$ s operáciou $a*b=a+b-1$ grupa?

3. Vieme, že $\mathbb R$ je vektorový priestor nad $\mathbb Q$ (s obvyklým sčitovaním a násobením). Ukážte, že v tomto vektorovom priestore sú vektory $1$, $\sqrt2$, $\sqrt5$ lineárne nezávislé.

4. a) Sú vektory $(1,1,1)$, $(1,2,3)$ a $(1,4,5)$ lineárne nezávislé nad $\mathbb R$?
b) Sú vektory $(1,2,1)$, $(1,3,1)$, $(2,1,1)$ a $(4,1,5)$ lineárne nezávislé nad $\mathbb R$?
c) Doplňte vektory $(2,1,1)$, $(1,1,3)$ na bázu priestoru $\mathbb R^3$.

5*. Dokážte, že v konečnej grupe, ktorá má párny počet prvkov, existuje prvok rôzny od neutrálneho prvku taký, že $a\circ a=e$.

Prvá úloha

Na obe časti zafunguje tento kontrapríklad:

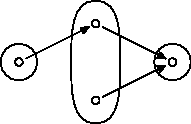
O príklad s injekciami si môžete prečítať aj tu: viewtopic.php?f=29&t=735

Niektorí z vás sa snažili tvrdenie dokázať a napísali ste mi tam niečo zhruba takéto:

$g(y_1)=g(y_2)$ $\Rightarrow$ $g(f(x_1))=g(f(x_2))$ $\Rightarrow$ $x_1=x_2$ $\Rightarrow$ $f(x_1)=f(x_2)$ $\Rightarrow$ $y_1=y_2$

Je pravda, že na dôkaz injektívnosti $g$ chceme z $g(y_1)=g(y_2)$ odvodiť $y_1=y_2$. Problematický je hneď prvý krok, kde ste prepísali $y_i$ ako $f(x_i)$. Nemáme ale zaručenú existenciu takého $x_i$, ktoré sa zobrazí na $y_i$.
Čiže takýto argument by bol zdôvodnením, že uvedené tvrdenie platí, ak pridáme ako ďalší predpoklad, že $f$ je surjektívne. (A teda ak chceme nájsť kontrapríklad, treba skúšať $f$, ktoré surjektívne nie je.)
Za takéto riešenie (ktoré by bolo správne iba pre surjektívne $f$) som dával 2 body. (Keď už spomínam bodovanie, tak už za to, keď z vášho riešenia bolo jasné, že viete aspoň definíciu injekcie resp. surjekcie, tak som dal 1 bod.)

Druhá úloha

Príklad zo skupiny A sa vyskytol v domácej úlohe: viewtopic.php?t=341
Často sa vyskytovala tá istá chyba, ktorá aj v d.ú.: Za inverzný prvok k $(a,b)$ ste prehlásili $(\frac1a,\frac1b)$. To nefunguje napríklad pre $(a,b)=(1,0)$.

Príklad zo skupiny B je vyriešený tu:
viewtopic.php?t=730
viewtopic.php?t=514

Tretia úloha

Riešenie

Pýtame sa vlastne, či platí: Ak $a+b\sqrt2+c\sqrt3=0$ pre $a,b,c\in\mathbb Q$, tak $a=b=c=0$.

Úpravou a umocnením na druhú dostaneme
$a+b\sqrt2=-c\sqrt3$
$a^2+2ab\sqrt2+2b^2=3c^2$
$2ab=\sqrt2=3c^2-a^2-2b^2$
Ak $ab\ne0$, tak dostaneme
$$\sqrt2=\frac{3c^2-a^2-2b^2}{2ab},$$
čo znamená, že $\sqrt2$ je racionálne číslo, a teda je to spor.

Zostáva nám teda prípad, že $ab=0$, t.j. $a=0$ alebo $b=0$.

Ak $a=0$, tak máme $b\sqrt2+c\sqrt3=0$. Po vynásobení $\sqrt2$ dostaneme
$2b+c\sqrt6=0$
$c\sqrt6=-2b$.
Ak $c\ne0$, tak dostaneme $\sqrt6-\frac{2b}c\in\mathbb{Q}$, čo je spor. Takže táto rovnosť môže nastať iba ak $c=0$. Z predošlej rovnice máme, že aj $b=0$ a zistili sme, že $\boxed{a=b=c=0}$.

Podobne ak $b=0$, tak máme $a+c\sqrt3=0$.
Pre $c\ne0$ by sme dostali $\sqrt3=-\frac ac \in\mathbb Q$, čo je spor.
Teda opäť, takáto rovnosť môže nastať iba ak $\boxed{a=b=c=0}$.

Komentáre k odovzdaným riešeniam

Niektorí ste sa dostali k tomu, že ste vyjadrili $\sqrt2$ alebo $\sqrt3$ ako podiel. Nijako ste neriešili otázku, či v menovateli nie je nula.

Niektorí z vás tvrdili, že $a+b\sqrt2+c\sqrt3$ je iracionálne číslo, lebo je to súčet racionálneho čísla $a$ a dvoch iracionálnych čísel $b\sqrt2$ a $c\sqrt3$. Toto nie je dobrý argument. Jednak nie je pravda, že súčet iracionálnych čísel je iracionálne číslo (kontrapríklad: $\sqrt2+(-\sqrt2)=0$.) Okrem toho, to že $b\sqrt2$ a $c\sqrt3$ sú iracionálne môžeme tvrdiť iba ak $b\ne0$, $c\ne0$.

Štvrtá úloha

Toto by mali byť úlohy, na ktoré sme sa naučili štandardné postupy. Aj tak tu niečo napíšem.

Začnem s časťou b: Tu stačilo povedať, že sú to 4 vektory v priestore dimenzie 4 a teda nutne musia byť lineárne závislé.

V úlohe a) sme sa naučili štandardné postupy:
* Zostavím sústavu zodpovedajúcu tomu, že $c_1\vec\alpha+c_2\vec\beta+c_3\vec\gamma=\vec0$. Ak má táto sústava iba nulové riešenie tak sú vektory lineárne nezávislé. Ak má aj nenulové riešenie, tak sú závislé.
* Vektory si poukladám do riadkov. Upravím na RTM. Ak dostanem nulový riadok, tak sú závislé. Ak dostanem nenulový riadok, tak sú nezávislé. (Zdôvodnenie: Z počtu nenulových riadkov RTM vidím dimenziu priestoru generovaného zadanými vektormi. Ak mám tri vektory v priestore dimenzie dva, tak musia byť závislé. Ak mám 3 vektory, ktoré generujú podpriestor dimenzie 3, tak sú lineárne nezávislé.)

V skupine A sa dalo aj zbadať, že súčet zadaných 3 vektorov je nulový vektor. (A podobne v úlohe b je súčet )

Riešenie cez sústavu

Skupina A:
$\left(\begin{array}{ccc|c}
1 & 1 & 3 & 0 \\
2 & 3 & 0 & 0 \\
3 & 3 & 4 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 3 & 0 \\
1 & 4 & 0 & 0 \\
1 & 1 & 3 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 3 & 0 \\
0 & 3 & 2 & 0 \\
0 & 0 & 0 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 3 & 0 \\
0 & 1 & 4 & 0 \\
0 & 0 & 0 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 0 & 4 & 0 \\
0 & 1 & 4 & 0 \\
0 & 0 & 0 & 0
\end{array}\right)$
Z tejto matice vieme vyčítať nenulové riešenie $(1,1,1)$. (Alebo aj všetky riešenie - sú to presne násobky tohoto vektora.)

$\left(\begin{array}{ccc|c}
1 & 1 & 1 & 0 \\
1 & 2 & 4 & 0 \\
1 & 3 & 5 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 1 & 0 \\
0 & 1 & 3 & 0 \\
0 & 2 & 4 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 1 & 0 \\
0 & 1 & 3 & 0 \\
0 & 1 & 2 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 1 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 2 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}\right)\sim$ $
\left(\begin{array}{ccc|c}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0
\end{array}\right)$
Vidíme, že sústava má iba nulové riešenie.

Riešenie pomocou úpravy na RTM:
$\begin{pmatrix}
1 & 2 & 3 \\
1 & 3 & 3 \\
3 & 0 & 4
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 2 & 3 \\
1 & 3 & 3 \\
1 & 0 & 3
\end{pmatrix}\sim$ $
\begin{pmatrix}
0 & 2 & 0 \\
0 & 3 & 0 \\
1 & 0 & 3
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 0 & 3 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{pmatrix}$

$\begin{pmatrix}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 4 & 5
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 1 & 1 \\
1 & 2 & 3 \\
0 & 2 & 2
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 1 & 1 \\
1 & 2 & 3 \\
0 & 1 & 1
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 0 & 0 \\
1 & 0 & 1 \\
0 & 1 & 1
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 1
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{pmatrix}\sim$ $
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}$

Piata úloha

V oboch skupinách je užitočné si ako prvé uvedomiť, že
$x\circ x=a$ $\Leftrightarrow$ $x=x^{-1}$.

Základná idea v skupine B je, že prvky môžeme "popárovať" do dvojíc prvok, inverzný prvok. Ak jediný prvok, ktorý je inverzný sám k sebe, je $e$, tak zistíme, že $G$ má nepárny počet prvkov.

V skupine sa riešenie dá stručne napísať aj takto:
Vieme, že pre každý prvok platí $x=x^{-1}$.
Ak si pamätáme z prednášky vzorec
$(x\circ y)^{-1}=y^{-1}\circ x^{-1}$,
tak pre takúto grupu dostaneme
$x\circ y=y\circ x$.

Dá sa to pomerne jednoducho aj tak, že nepoužijeme nič iné ako definíciu grupy.
Platia súčasne nasledujúce dve rovnosti
$(x\circ y)\circ(x\circ y)=e$
$(x\circ y)\circ(y\circ x)=e$ Z rovnosti
$(x\circ y)\circ(x\circ y)=(x\circ y)\circ(y\circ x)$
dostaneme
$x\circ y=y\circ y$
buď tak, že obe strany vynásobíme zľava $(x\circ y)^{-1}$ (čo je v tomto prípade to isté ako $(x\circ y)$); alebo môžeme využiť zákony o krátení.