msleziak.com

Pretože ste sa (matfyzáci) sťažovali, že vám budú chýbať úlohy, ktoré sme preriešili na minulom cviku (keď ste mali dekanské voľno kvôli promóciám), tak skúsim aspoň nejaké príklady (ktoré stihnem) dať aj sem na fórum.

EDIT: Ostatné úlohy z toho istého cvičenia sú tu a tu.

$\newcommand{\Zobr}[3]{#1\colon#2\to#3}\newcommand{\Lra}{\Leftrightarrow}\newcommand{\Ra}{\Rightarrow}\newcommand{\Invobr}[2]{\inv{#1}(#2)}\newcommand{\Obr}[2]{#1[#2]}$

Predpoklady, ktoré platia vo všetkých častiach: $\Zobr fXY$, $\Zobr gYZ$ sú zobrazenia, $A,B\subseteq X$, $C,D\subseteq Y$, $E\subseteq Z$, $A_i\subseteq X$ a $B_i\subseteq Y$ pre každé $i\in I$.

Úloha 1: Dokázať, že: $\Obr f{A\cap B}\subseteq \Obr fA \cap \Obr fB$ a ak $f$ je injektívne, tak $\Obr f{A\cap B} = \Obr fA \cap \Obr fB$;

Najprv pracujme s ľubovoľnou funkciou $f$. Chceme ukázať, že každý prvok z $\Obr f{A\cap B}$ musí patriť aj do $\Obr fA \cap \Obr fB$.

Nech teda $y\in\Obr f{A\cap B}$. To teda znamená, že $y=f(x)$ pre nejaké $x\in A\cap B$. Čiže $y$ je obrazom takého $x$, ktoré patrí do $A$ aj do $B$. Z toho vyplýva, že $y=f(x)$ patrí do $\Obr fA$ a súčasne do $\Obr fB$. Čo znamená, že $y\in \Obr fA\cap \Obr fB$.

Skúsme teraz formálnejšie zapísať to, čo sme napísali pred chvíľou slovne, navyše sa skúsme pozrieť, či niektoré implikácie nahradiť ekvivalenciami. (Poznámka: Keď odovzdávate úlohu/píšete písomku, mne - ako opravujúcemu - je v podstate jedno, či to rozpíšte slovne alebo použijete stručnejší zápis pomocou logických spojok. Dôležité je, aby bol váš zápis zrozumiteľný a aby bolo jasné, čo vlastne robíte.)

$y\in\Obr f{A\cap B}$ $\Lra$ $(\exists x\in A\cap B) y=f(x)$ $\Lra$ $(\exists x) (x\in A\cap B) \land y=f(x)$ $\Lra$ $(\exists x) (x\in A) \land (x\in B) \land y=f(x)$ $\Ra$ $[(\exists x) (x\in A) \land y=f(x)] \land [(\exists x) (x\in B) \land f(x)]$ $\Lra$ $[(\exists x\in A) y=f(x)] \land (\exists x\in B) y=f(x)$ $\Lra$ $(y\in\Obr fA) \land (y\in\Obr fB)$ $\Lra$ $y\in \Obr fA \cap \Obr fB$

Mohli sme teda vo všetkých krokoch napísať ekvivalenciu, jedinou výnimkou je
$$(\exists x) (x\in A) \land (x\in B) \land y=f(x) \Ra [(\exists x) (x\in A) \land y=f(x)] \land [(\exists x) (x\in B) \land f(x)].$$
Prečo tu nemôžeme písať implikáciu sprava doľava? Na prvý pohľad by sa zdalo, že ak platí podmienka vpravo, vieme, že $x$ patrí do $A$ a zobrazí na $f(x)$, a súčasne $x$ patrí do $B$ a zobrazí sa na $f(x)$. Takéto $x$ predsa patrí do $A\cap B$ a zobrazí sa na $y$...???

Treba dať pozor na to, že keď máme výrok tvaru $[(\exists x)P(x)]\land[(\exists x)Q(x)]$, tak vieme, že existuje nejaký prvok, ktorý má vlastnosť $P(x)$ aj to, že existuje prvok, ktorý má vlastnosť $Q(x)$, ale nemusí to nutne byť jeden a ten istý prvok. (Zhodou okolnosti sme ho tu - v dvoch navzájom nesúvisiacich častiach výroku - označili tým istým písmenom.) Aby nás to neplietlo, radšej si teda túto podmienku prepíšme tak, že použijeme rôzne premenné: $[(\exists x_1) (x_1\in A) \land y=f(x_1)] \land [(\exists x_2) (x_2\in B) \land f(x_2)]$.

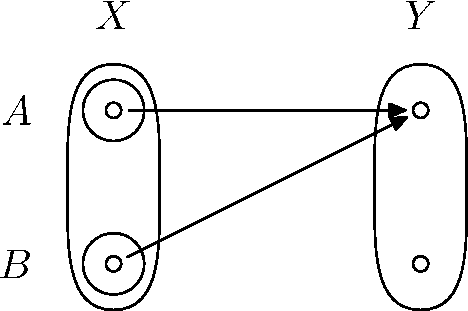
Teraz je už jasnejšie, že tento výrok skutočne nemožno obrátiť. Navyše by ste určite vedeli ľahko nájsť aj kontrapríklad - konkrétnu funkciu, pre ktorú $\Obr f{A\cap B}\ne\Obr fA \cap \Obr fB$. (Ako naznačuje druhá časť zadania, asi treba skúšať medzi funkciami, ktoré nie sú injektívne.) Čo sa však stane, ak vieme, že $f$ je injektívna? Vtedy máme $f(x_1)=y$ pre nejaké $x_1\in A$ a $f(x_2)=y$ pre nejaké $x_2\in A$. Z injektívnosti však dostaneme
$$f(x_1)=y=f(x_2) \Ra x_1=x_2,$$
teda $x_1$ aj $x_2$ je ten istý prvok. (A môžeme ho rovno označiť $x$.) Zistili sme, že existuje $x$ také, že $(x\in A) \land (x\in B) \land y=f(x)$. To je však to isté ako, že $(x\in A\cap B) \land y=f(x)$. A existencia takéhoto $x$ znamená, že $y\in f[A\cap B]$.

Vidíme teda, že pre injektívne zobrazenie $f$ platí $$\Obr f{A\cap B}=\Obr fA\cap \Obr fB.$$

EDIT: Nejaké poznámky k tejto úlohe sa dajú nájsť aj tu: viewtopic.php?t=1256

*******

Úloha 2: Dokážte: $\Obr f{\bigcup_{i\in I} A_i} = \bigcup_{i\in I} \Obr f{A_i}$.

Tento príklad už skúsme zapísať stručnejšie
$y\in \Obr f{\bigcup_{i\in I} A_i}$ $\Lra$ $(\exists x) x\in \bigcup_{i\in I} A_i\land y=f(x)$ $\Lra$ $(\exists x) (\exists i\in I) x\in A_i\land y=f(x)$ $\overset{(*)}{\Lra}$ $(\exists i\in I)(\exists x) x\in A_i\land y=f(x)$ $\Lra$ $(\exists i\in I) y\in\Obr f{A_i}$ $\Lra$ $y\in\bigcup_{i\in I} \Obr f{A_i}$

Ekvivalencia označená (*) platí vďaka tomu, že pre ľubovoľný výrok $P(x,y)$ platí $(\exists x)(\exists y)P(x,y) \Lra (\exists y)(\exists x)P(x,y)$. (Skúste si rozmyslieť - "kvetinková metóda".)

V prípade problémov so zobrazením skrytých častí (spoiler) skúste použiť tento návod.

Skúsme sa pozrieť ešte na iný spôsob, ako sa dá dokázať prvá časť tejto úlohy:

Úloha 1: Dokázať, že: $\Obr f{A\cap B}\subseteq \Obr fA \cap \Obr fB$.

Použijeme nasledovné pomerne jednoduché pozorovanie:

Lema:Ak $C\subseteq D$ sú podmnožiny $X$ a $\Zobr fXY$, tak $\Obr fC \subseteq \Obr fD$.

Dôkaz lemy. Ak $y\in \Obr fC$, znamená to, že $y=f(x)$ pre nejaké $x\in C$. Pretože $C\subseteq D$, každé takéto $x$ je súčasne aj prvkom $D$. To znamená, že $y\in\Obr fD$. $\square$

Keď už máme dokázané túto lemu, tak pôvodnú úlohu môžeme vyriešiť takto:

• Všimneme si, že $A\cap B\subseteq A$ a $A\cap B\subseteq B$.
• Z lemy potom máme $\Obr f{A\cap B}\subseteq \Obr fA$ a $\Obr f{A\cap B}\subseteq \Obr fB$.
• Ak platia obe uvedené inklúzie, tak platí aj $\Obr f{A\cap B}\subseteq \Obr fA \cap \Obr fB$.