ErikVarga108 wrote:
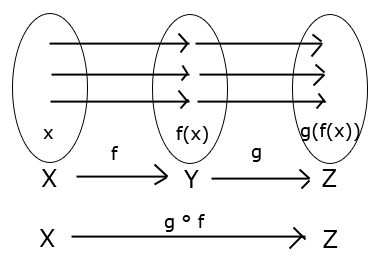
Vychádzam z predpokladu, že $g\circ f$ je injekcia. Potom by malo platiť:
$g\circ f(x) = g\circ f(y)$
$g(f(x)) = g(f(y))$
$f(x) = f(y)$
Keďže zobrazenie $g\circ f$ je injekcia, musí platiť aj $x = y$ (malo by to vychádzať z definície) a preto si myslím, že funkcia $f$ je injektívna.
Dohodnime sa, že táto prvá časť je ok (=ok z toho hľadiska, či za ňu dostanete body), aj keď pokec vysvetľujúci váš postup nie je celkom správny.
Správnejšie by bolo povedať, že: keď chceme dokázať, že $g\circ f$ je injekcia, tak vlastne chceme overiť implikáciu $g\circ f(x)=g\circ f(y)$ $\Rightarrow$ $x=y$.
Takže začneme tým, že budeme predpokladať, že pre nejaké $x$, $y$ platí $g\circ f(x)=g\circ f(y)$ a budeme sa snažiť odvodiť $x=y$.
Po tomto úvode už všetky ďalšie kroky, ktoré ste napísali, sedia s tým, čo chceme robiť.
OPRAVA: Mal som napísať toto. Dokazujeme, že $f$ je injekcia. (Omylom som napísal $g\circ f$.)
Teda vychádzame z predpokladu $f(x)=f(y)$.
Z neho dostaneme, že aj $g(f(x))=g(f(y))$.
Na tomto mieste využijeme, že $g\circ f$ je injekcia a dostaneme $x=y$-
Skontrolovali sme, že z $f(x)=f(y)$ vyplýva $x=y$.
ErikVarga108 wrote:
Platí táto implikácia aj opačne? Teda: platí, že ak $f$ je injekcia, tak aj $g\circ f$ je injekcia ?
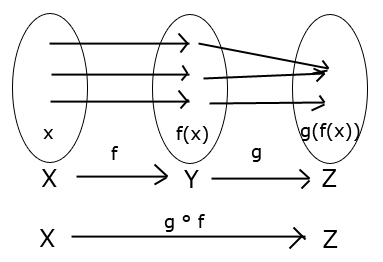
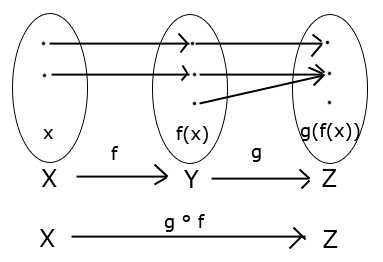
Myslím, že neplatí, lebo v prípade, že by funkcia $g$ nebola injektívna, nemohlo by zobrazenie $g\circ f$ byť injektívne.
Inými slovami, aby sme dostali injektívne zložené zobrazenie, obe funkcie, vrátane funkcie $g$ musia byť injektívne. Ak to tak nie je, rád sa nechám vyviesť z omylu

Ak si myslíte, že to platí, mali by ste to aj dokázať.
V skutočnosti neplatí, to čo ste tvrdili, t.j. nie je pravda, že: $g\circ f$ je injektívne $\Rightarrow$ $g$ je injektívne.
Aby som vás presvedčil, že to je tak, mal by som nájsť konkrétny príklad funkcií takých, že zloženie $g\circ f$ je injektívne, ale funkcia $g$ nie je injektívna.
Nebudem sem však (aspoň zatiaľ) taký príklad písať, lebo toto je vlastne súčasť úlohy. Mali ste si rozmyslieť, či táto vec platí (vy ste napísali, že áno; ja už som vám prezradil, že nie). Ešte treba nejako zdôvodniť, že neplatí - t.j. nájsť konkrétny príklad, na ktorom to ukážete. (Resp. ak ste presvedčený, že to platí - a minimálne keď ste posielali predošlý post, tak ste si zjavne mysleli, že to platí - tak by tu mal byť dôkaz, že to je naozaj tak. Skúsiť tvrdenie dokazovať možno tiež nemusí byť zlá taktika, aj ak ešte nevieme či platí. Môže sa stať, že pri dôkaze narazíme na problémy a keď budeme vidieť v čom presne bol problém pri dôkaze, ta nám to môže pomôcť nájsť kontrapríklad.)