EDIT: Ostatné úlohy z toho istého cvičenia sú tu a tu.
$\newcommand{\Zobr}[3]{#1\colon#2\to#3}\newcommand{\Lra}{\Leftrightarrow}\newcommand{\Ra}{\Rightarrow}\newcommand{\Invobr}[2]{\inv{#1}(#2)}\newcommand{\Obr}[2]{#1[#2]}$
Predpoklady, ktoré platia vo všetkých častiach: $\Zobr fXY$, $\Zobr gYZ$ sú zobrazenia, $A,B\subseteq X$, $C,D\subseteq Y$, $E\subseteq Z$, $A_i\subseteq X$ a $B_i\subseteq Y$ pre každé $i\in I$.
Úloha 1: Dokázať, že: $\Obr f{A\cap B}\subseteq \Obr fA \cap \Obr fB$ a ak $f$ je injektívne, tak $\Obr f{A\cap B} = \Obr fA \cap \Obr fB$;
Najprv pracujme s ľubovoľnou funkciou $f$. Chceme ukázať, že každý prvok z $\Obr f{A\cap B}$ musí patriť aj do $\Obr fA \cap \Obr fB$.
Nech teda $y\in\Obr f{A\cap B}$. To teda znamená, že $y=f(x)$ pre nejaké $x\in A\cap B$. Čiže $y$ je obrazom takého $x$, ktoré patrí do $A$ aj do $B$. Z toho vyplýva, že $y=f(x)$ patrí do $\Obr fA$ a súčasne do $\Obr fB$. Čo znamená, že $y\in \Obr fA\cap \Obr fB$.
Skúsme teraz formálnejšie zapísať to, čo sme napísali pred chvíľou slovne, navyše sa skúsme pozrieť, či niektoré implikácie nahradiť ekvivalenciami. (Poznámka: Keď odovzdávate úlohu/píšete písomku, mne - ako opravujúcemu - je v podstate jedno, či to rozpíšte slovne alebo použijete stručnejší zápis pomocou logických spojok. Dôležité je, aby bol váš zápis zrozumiteľný a aby bolo jasné, čo vlastne robíte.)
$y\in\Obr f{A\cap B}$ $\Lra$ $(\exists x\in A\cap B) y=f(x)$ $\Lra$ $(\exists x) (x\in A\cap B) \land y=f(x)$ $\Lra$ $(\exists x) (x\in A) \land (x\in B) \land y=f(x)$ $\Ra$ $[(\exists x) (x\in A) \land y=f(x)] \land [(\exists x) (x\in B) \land f(x)]$ $\Lra$ $[(\exists x\in A) y=f(x)] \land (\exists x\in B) y=f(x)$ $\Lra$ $(y\in\Obr fA) \land (y\in\Obr fB)$ $\Lra$ $y\in \Obr fA \cap \Obr fB$
Mohli sme teda vo všetkých krokoch napísať ekvivalenciu, jedinou výnimkou je
$$(\exists x) (x\in A) \land (x\in B) \land y=f(x) \Ra [(\exists x) (x\in A) \land y=f(x)] \land [(\exists x) (x\in B) \land f(x)].$$
Prečo tu nemôžeme písať implikáciu sprava doľava? Na prvý pohľad by sa zdalo, že ak platí podmienka vpravo, vieme, že $x$ patrí do $A$ a zobrazí na $f(x)$, a súčasne $x$ patrí do $B$ a zobrazí sa na $f(x)$. Takéto $x$ predsa patrí do $A\cap B$ a zobrazí sa na $y$...???
Treba dať pozor na to, že keď máme výrok tvaru $[(\exists x)P(x)]\land[(\exists x)Q(x)]$, tak vieme, že existuje nejaký prvok, ktorý má vlastnosť $P(x)$ aj to, že existuje prvok, ktorý má vlastnosť $Q(x)$, ale nemusí to nutne byť jeden a ten istý prvok. (Zhodou okolnosti sme ho tu - v dvoch navzájom nesúvisiacich častiach výroku - označili tým istým písmenom.) Aby nás to neplietlo, radšej si teda túto podmienku prepíšme tak, že použijeme rôzne premenné: $[(\exists x_1) (x_1\in A) \land y=f(x_1)] \land [(\exists x_2) (x_2\in B) \land f(x_2)]$.
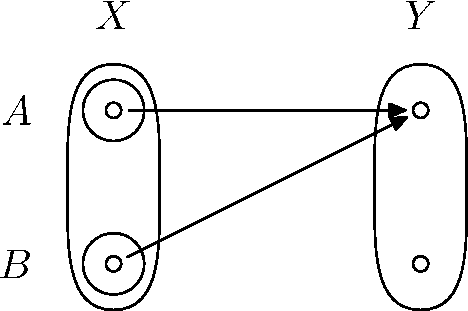
Teraz je už jasnejšie, že tento výrok skutočne nemožno obrátiť. Navyše by ste určite vedeli ľahko nájsť aj kontrapríklad - konkrétnu funkciu, pre ktorú $\Obr f{A\cap B}\ne\Obr fA \cap \Obr fB$. (Ako naznačuje druhá časť zadania, asi treba skúšať medzi funkciami, ktoré nie sú injektívne.)
Spoiler:
$$f(x_1)=y=f(x_2) \Ra x_1=x_2,$$
teda $x_1$ aj $x_2$ je ten istý prvok. (A môžeme ho rovno označiť $x$.) Zistili sme, že existuje $x$ také, že $(x\in A) \land (x\in B) \land y=f(x)$. To je však to isté ako, že $(x\in A\cap B) \land y=f(x)$. A existencia takéhoto $x$ znamená, že $y\in f[A\cap B]$.
Vidíme teda, že pre injektívne zobrazenie $f$ platí $$\Obr f{A\cap B}=\Obr fA\cap \Obr fB.$$
EDIT: Nejaké poznámky k tejto úlohe sa dajú nájsť aj tu: viewtopic.php?t=1256
*******
Úloha 2: Dokážte: $\Obr f{\bigcup_{i\in I} A_i} = \bigcup_{i\in I} \Obr f{A_i}$.
Tento príklad už skúsme zapísať stručnejšie
$y\in \Obr f{\bigcup_{i\in I} A_i}$ $\Lra$ $(\exists x) x\in \bigcup_{i\in I} A_i\land y=f(x)$ $\Lra$ $(\exists x) (\exists i\in I) x\in A_i\land y=f(x)$ $\overset{(*)}{\Lra}$ $(\exists i\in I)(\exists x) x\in A_i\land y=f(x)$ $\Lra$ $(\exists i\in I) y\in\Obr f{A_i}$ $\Lra$ $y\in\bigcup_{i\in I} \Obr f{A_i}$
Ekvivalencia označená (*) platí vďaka tomu, že pre ľubovoľný výrok $P(x,y)$ platí $(\exists x)(\exists y)P(x,y) \Lra (\exists y)(\exists x)P(x,y)$. (Skúste si rozmyslieť - "kvetinková metóda".)