Riešenia
Skupina A
Jednoduchý príklad je zobrazenie, ktoré vymieňa dva prvky; napríklad $X=\{0,1\}$ a $f(0)=1$, $f(1)=0$.
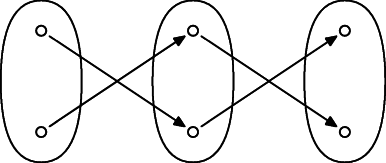
Iné príklady: $f\colon\mathbb R\to\mathbb R$, $f(x)=-x$
Zobrazenia s touto vlastnosťou sa volajú
involúcie.
Skupina B
Opäť sa dá nájsť jednoduchý príklad: $X=\{0,1\}$, $f(0)=f(1)=0$
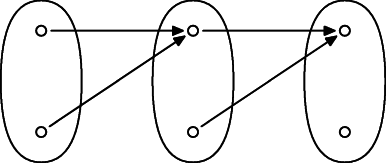
Úplne podobne to zafunguje, ak si vezmeme ľubovoľnú množinu $X$ a nejaké konštantné zobrazenie. (Pretože chceme $f\ne id_X$, potrebujeme aby $X$ nebola jednoprvková množina.)
Môžeme si všimnúť, že ak chceme nájsť takýto príklad, tak $f$ nemôže byť bijektívne. Vtedy by sme z $f\circ f=f$ dostali po zložení s $f^{-1}$, že $f=id$.
Pri trochu väčšej námahe sa dá prísť na to, že $f$ nemôže byť injektívne a ani surjektívne. (Skúste sa pozrieť na príklady, ktoré sme mali k zobrazeniam. Ak sa pozriete na dôkazové úlohy, tak sa vám možno padnú do oka nejaké, ktoré by mohli pomôcť zdôvodniť, že $f\circ f=f$ implikuje $f=id$ v prípade, že $f$ je surjektívne resp. že $f$ je injektívne.)
Skupina C
Stačí zobrať príklad zo skupiny B. (A položiť $g=f$.)
Poznámky k odovzdaným riešeniam
V podstate väčšina ľudí buď nemala nič alebo tam mala správny kontrapríklad.
Niektorí ste sa snažili dokázať, že také funkcie neexistuje. (Snáď príklady, ktoré tu sú, vás presvedčia že existujú.)

