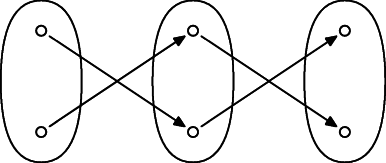
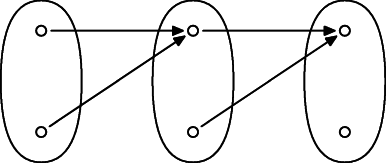
Injekcie, surjekcie a skladanie
Posted: Mon Oct 23, 2017 2:29 pm
Zadania
Skupina A
viewtopic.php?t=493
viewtopic.php?t=735
Skupina A
Skupina BNájdite príklad množiny $X$ a zobrazenia $f\colon X\to X$ takých, že $f\ne id_X$ a platí $$f\circ f=id_X.$$
Skupina CNájdite príklad množiny $X$ a zobrazenia $f\colon X\to X$ takých, že $f\ne id_X$ a platí $$f\circ f=f.$$
Ak by ste sa chceli pozrieť na staršie zadania písomkových úloh na tieto témy:Nájdite príklad množiny $X$ a zobrazení $f,g\colon X\to X$ takých, že $g\ne id_X$ a platí $$f\circ g=f.$$
viewtopic.php?t=493
viewtopic.php?t=735