Úloha 1.2 Surjekcia

[ErikVarga108]

Úloha 1.2. Dokážte: Ak $g \circ f $ je surjekcia, tak aj $g$ je surjekcia. Platí aj opačná implikácia? Musí byť $f$ surjekcia?

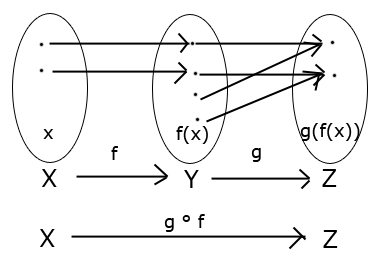
$f: X \rightarrow Y$
$g: Y \rightarrow Z$
$g\circ f: X \rightarrow Z$

Surjekcia: Aby $g$ bola surjekcia, pre každé $z\in Z$ treba nájsť $y\in Y$, ktoré sa na neho zobrazí.

Viem, že $g\circ f$ je zložené zobrazenie. Môžem teda predpokladať, že pre každé $z\in Z$ bude existovať aj nejaké $x\in X$, ktoré sa zobrazí na $Y$.

$g\circ f$ je surjekcia, preto môžem povedať toto: $(\forall z\in Z) (\exists x): g(f(x)) = z$, pričom všetky prvky $f(x)$ sú z množiny $Y$, teda množina $Z$ je celá obsadená prvkami množiny $Y$ (to je to, čo sme chceli zistiť), a teda funkcia $g$ je surjektívna.

-----

Platí opačná implikácia? Musí byť $f$ surjektívna?

Nemusí, $f$ nemá vplyv na to, či sa obsadí celá množina $Z$:


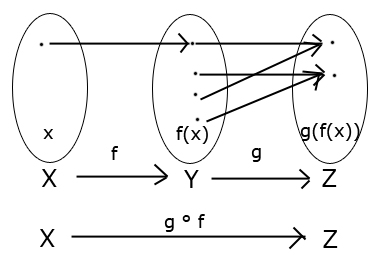
Príklad:
$X:$ {$0$}
$Y:$ {$1, 2, 3, 4$}
$Z:$ {$1, 2$}

$f: X \rightarrow Y$
$g: Y \rightarrow Z$
$g\circ f: X \rightarrow Z$

$f(x) = x+1$ (0 sa zobrazí na 1) - neobsadí celú množinu $Y$, preto $f$ nie je surjektívna
$g(f(x)):$
- ak $f(x)$ je nepárne číslo: $g(f(x)) = 1$ (1, 3 sa zobrazia na 1)
- ak $f(x)$ je párne číslo: $g(f(x)) = 2$ (2, 4 sa zobrazia na 2) - množina $Z$ sa celá obsadí prvkami z $Y$, preto $g$ je surjektívna

$g\circ f:$ je surjektívna (množina $Z$ je plne obsadená) napriek tomu, že $f$ surjektívna nie je (akoby to záviselo len od $g$).

[Martin Sleziak]

S prvou časťou súhlasím, ale kontrapríklad nie je dobre. Všimnite si, že funkcia $g\circ f$, ktorú ste navrhli, nie je surjektívna. (Zobrazenie $g\circ f$ vyzerá tak, že 1 sa zobrazí na 1; na prvok 2 sa nezobrazí nič. Aj všeobecne by malo byť vcelku jasné, že ak existuje surjekci $X\to Y$, tak množina $X$ musí mať aspoň toľko prvkov ako množina $Y$. Teda určite nebude existovať surjekcia z jednoprvkovej množiny do dvojprvkovej.)

[ErikVarga108]

Toto by mohlo byť lepšie (keď sa na to teraz tak pozerám, ten prvý obrázok som veru nedomyslel):


$X:$ {$0, 1$}
$Y:$ {$1, 2, 3, 4$}
$Z:$ {$1, 2$}

$f: X \rightarrow Y$
$g: Y \rightarrow Z$
$g\circ f: X \rightarrow Z$

$f(x) = x+1$ (0 sa zobrazí na 1, 1 na 2)
$g(f(x)):$
- ak $f(x)$ je nepárne číslo: $g(f(x)) = 1$ (1, 3 sa zobrazia na 1)
- ak $f(x)$ je párne číslo: $g(f(x)) = 2$ (2, 4 sa zobrazia na 2)

$g\circ f:$ napokon zobrazí 2 na 2 a 1 na 1.

[Martin Sleziak]

Ok, značím si 1 bod.