Asociatívnosť symetrickej diferencie
Posted: Sun Oct 27, 2024 9:39 am
Pripomeňme, že symetrická diferencia. je definovaná takto:
$$A\triangle B=(A\setminus B)\cup(B\setminus A).$$
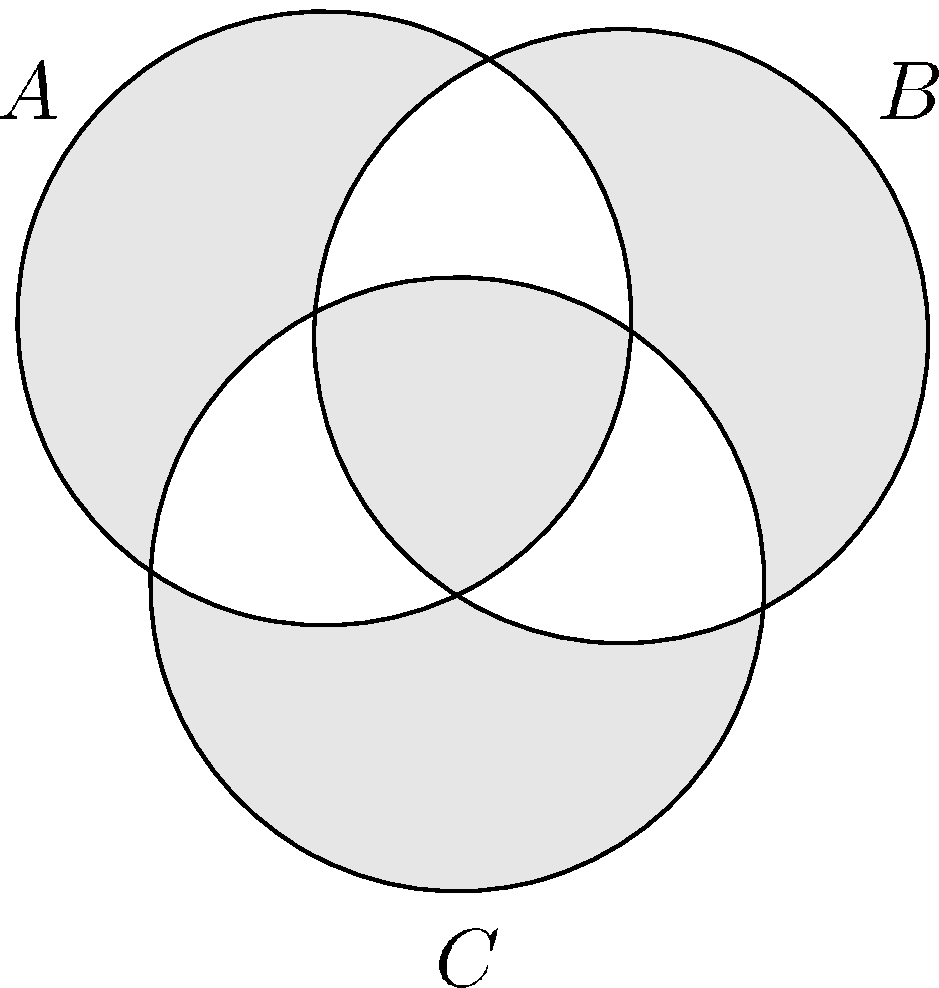
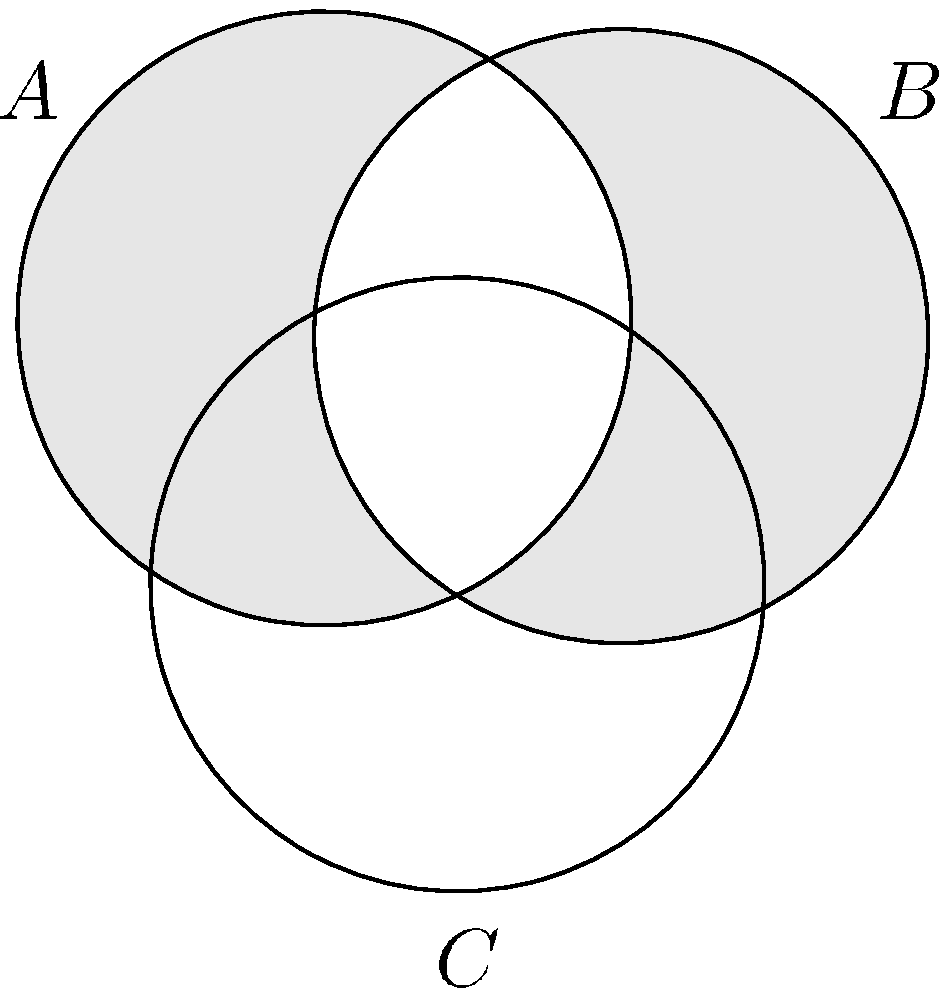
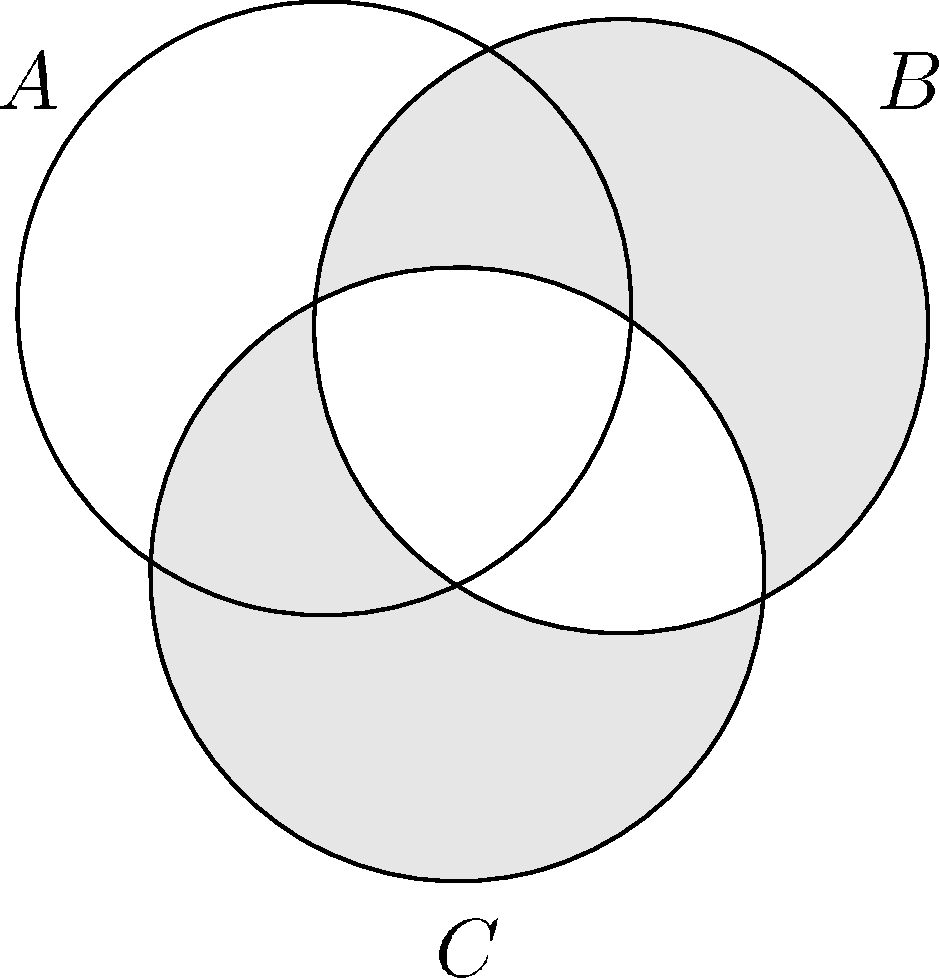
V jednej úlohe sa nám hodilo vedieť, že symetrická diferencia je asociatívna, t.j. že pre ľubovoľné množiny $A$, $B$, $C$ platí
$$A\triangle (B\triangle C)=(A\triangle B)\triangle C.$$
Poďme sa pozrieť na nejaké možnosti, ako sa to dá zdôvodniť. (Ktorúkoľvek z možností spomenutých nižšie by som v domácej úlohe bez problémov akceptoval ako riešenie.)
Súčasne, ak sa popozeráte po internete, tak nájdete dôkaz tohto tvrdenia na mnohých miestach. Tu je pár liniek:
Tu je linka na text a pridám aj linku na slajdy.
Nájdete tam aj zdôvodnenie toho, že symetrická diferencia je asociatívna (pomocou Vennových diagramov aj pomocou tabuľky pravdivostných hodnôt).
Je to veľmi podobné ako to, čo píšem sem na fórum - ale ak by sa vám to náhodou čítalo v PDF-ku, tak môžete pozrieť tam.
$$A\triangle B=(A\setminus B)\cup(B\setminus A).$$
V jednej úlohe sa nám hodilo vedieť, že symetrická diferencia je asociatívna, t.j. že pre ľubovoľné množiny $A$, $B$, $C$ platí
$$A\triangle (B\triangle C)=(A\triangle B)\triangle C.$$
Poďme sa pozrieť na nejaké možnosti, ako sa to dá zdôvodniť. (Ktorúkoľvek z možností spomenutých nižšie by som v domácej úlohe bez problémov akceptoval ako riešenie.)
Súčasne, ak sa popozeráte po internete, tak nájdete dôkaz tohto tvrdenia na mnohých miestach. Tu je pár liniek:
- Symmetric Difference is Associative - ProofWiki
- Associativity of symmetric set difference - Mathematics Stack Exchange
- Symmetric difference using Venn diagrams (Discrete Math) - Mathematics Stack Exchange
Tu je linka na text a pridám aj linku na slajdy.
Nájdete tam aj zdôvodnenie toho, že symetrická diferencia je asociatívna (pomocou Vennových diagramov aj pomocou tabuľky pravdivostných hodnôt).
Je to veľmi podobné ako to, čo píšem sem na fórum - ale ak by sa vám to náhodou čítalo v PDF-ku, tak môžete pozrieť tam.