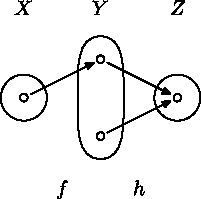
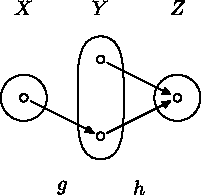
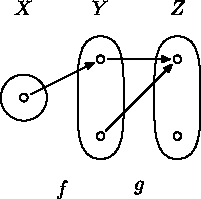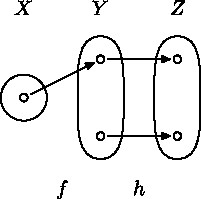Aspoň prvá časť sa dá nájsť na fóre - v častiach k iným predmetom:Skupina A: $\newcommand{\Zobr}[3]{#1\colon #2\to#3}$Nech $\Zobr{f,g}XY$ a $\Zobr hYZ$ sú zobrazenia.
a) Dokážte, že ak $h$ je injekcia, tak z rovnosti $h\circ f=h\circ g$ vyplýva $f=g$.
b) Ukážte na príklade, že tvrdenie z prvej časti úlohy neplatí ak vynecháme predpoklad, že $h$ je injekcia.
Skupina B: Nech $\Zobr fXY$ a $\Zobr{g,h}YZ$ sú zobrazenia.
a) Dokážte, že ak $f$ je surjekcia, tak z rovnosti $g\circ f=h\circ f$ vyplýva $g=h$.
b) Ukážte na príklade, že tvrdenie z prvej časti úlohy neplatí ak vynecháme predpoklad že $f$ je surjekcia.
https://msleziak.com/forum/viewtopic.php?t=561#p1444
https://msleziak.com/forum/viewtopic.php?t=1447
https://msleziak.com/forum/viewtopic.php?t=1312 a https://msleziak.com/forum/viewtopic.php?t=1311
Aj tak radšej začnem nový topic, keďže chcem niečo napísať aj ku druhej časti (nájdenie kontrapríkladov) a k niektorým odovzdaným riešeniam a tomu aké chyby sa vyskytli.
Všeobecná poznámka: Keď niečo dokazujete, tak sa oplatí pozrieť sa na to, či ste naozaj použili všetky predpoklady. (A práve časť b vám mala pomôcť všimnúť si, že predpoklad o injektívnosti resp. o surjektívnosti určite treba v dôkaze použiť; bez neho toto tvrdenie neplatí.)
Čiže ak ste dokázali nejako toto tvrdenie a v dôkaze nikde nevidíte použitý predpoklad že zobrazenie je injekcia/surjekcia, tak je rozumné sa pozrieť či tam nie je nejaký problém. (Ako som spomenul, ak ste to dokázali bez tohoto predpokladu, tak je dôkaz nesprávny. Ale skôr by som považoval za dôležité to, že veci ktoré máte na písomkách sú veci, ktoré by sme vás chceli naučiť a ktorým by ste mali po absolvovaní tohoto predmetu ako-tak rozumieť. A ak sa vám zdá váš dôkaz správny - a súčasne máte pre sebou kontrapríklad ukazujúci že to čo ste dokázali nemôže platiť - tak je pravdepodobné že môžete mať v týchto veciach nejaké nejasnosti.)